题目内容
19．
如图，在△ABC中，D为BC的中点，E为AD的中点，直线BE与边AC交于点F，若AD=BC=6，则$\overrightarrow{AB}•\overrightarrow{CF}$=-18．
分析 建立坐标系，设∠ADC=α，求出各点坐标，代入向量的数量积运算公式计算即可．
解答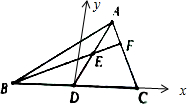 
解：以BC为x轴，以BC的中垂线为y轴建立平面直角坐标系，
设∠ADC=α，则A（6cosα，6sinα），E（3cosα，3sinα），C（3，0），B（-3，0），
设F（a，b），则$\left\{\begin{array}{l}{\frac{b}{a+3}=\frac{3sinα}{3cosα+3}}\\{\frac{b}{a-3}=\frac{6sinα}{6cosα-3}}\end{array}\right.$，解得a=4cosα+1，b=4sinα，
∴$\overrightarrow{AB}$=（-3-6cosα，-6sinα），$\overrightarrow{CF}$=（4cosα-2，4sinα），
∴$\overrightarrow{AB}•\overrightarrow{CF}$=（-3-6cosα）（4cosα-2）-24sin2α=-24cos2α+6-24sin2α=6-24=-18．
故答案为：-18．
点评 本题考查了平面向量的数量积运算，属于中档题．
练习册系列答案
相关题目
9．
已知f（x）=Asin （ω x+φ）+（A＞0，ω＞0，|φ|＜π}）的图象如图所示，则f（3π）=（ ）
已知f（x）=Asin （ω x+φ）+（A＞0，ω＞0，|φ|＜π}）的图象如图所示，则f（3π）=（ ）| A． | -$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
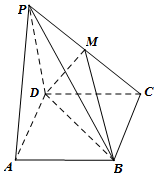如图，四棱锥P-ABCD中，底面ABCD是矩形，平面PAD⊥平面ABCD，且△PAD是边长为2的等边三角形，$PC=\sqrt{13}$，点M是PC的中点．