题目内容
18．二面角α-AB-β的平面角是锐角θ，M∈α，MN⊥β，N∈β，C∈AB，∠MCB为锐角，则（ ）| A． | ∠MCN＜θ | B． | ∠MCN=θ | ||
| C． | ∠MCN＞θ | D． | 以上三种情况都有可能 |
分析 过M作MO⊥AB于O，过N作NO⊥AB于O，则∠MON=θ，连接CN，在Rt△CMN中，sin∠MCN=$\frac{MN}{CN}$$＜\frac{MN}{ON}=sinθ$．即可判定．
解答 
解：如图，过M作MO⊥AB于O，过N作NO⊥AB于O，则∠MON=θ，
连接CN，在Rt△CON中，有CM＞OM，
在Rt△CMN中，sin∠MCN=$\frac{MN}{CM}＜\frac{MN}{OM}$=sinθ，∴∠MCN＜θ，
故选：A．
点评 本题考查了空间角的大小判定，考查了转化思想，属于中档题．
练习册系列答案
相关题目
8．
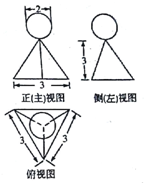某几何体的三视图如图所示，则该几何体的体积为（ ）
某几何体的三视图如图所示，则该几何体的体积为（ ）| A． | $\frac{4π}{3}$+$\frac{9\sqrt{3}}{4}$ | B． | $\frac{4π}{3}$+$\frac{27\sqrt{3}}{4}$ | C． | $\frac{8π}{3}$+$\frac{9\sqrt{3}}{4}$ | D． | $\frac{8π}{3}$+$\frac{27\sqrt{3}}{4}$ |
9．
已知f（x）=Asin （ω x+φ）+（A＞0，ω＞0，|φ|＜π}）的图象如图所示，则f（3π）=（ ）
已知f（x）=Asin （ω x+φ）+（A＞0，ω＞0，|φ|＜π}）的图象如图所示，则f（3π）=（ ）| A． | -$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
3．已知梯形ABCD中，∠ABC=∠BAD=$\frac{π}{2}$，AB=BC=1，AD=2，P是DC的中点，则|$\overrightarrow{PA}$+2$\overrightarrow{PB}$|=（ ）
| A． | $\frac{\sqrt{82}}{2}$ | B． | 2$\sqrt{5}$ | C． | 4 | D． | 5 |
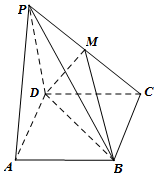如图，四棱锥P-ABCD中，底面ABCD是矩形，平面PAD⊥平面ABCD，且△PAD是边长为2的等边三角形，$PC=\sqrt{13}$，点M是PC的中点．