题目内容
1.在菱形ABCD中,A=60°,AB=2$\sqrt{3}$,将△ABD沿BD折起到△PBD的位置,若二面角P-BD-C的大小为120°,三棱锥P-BCD的外接球球心为O,BD的中点为E,则OE=( )| A. | 1 | B. | 2 | C. | $\sqrt{7}$ | D. | 2$\sqrt{7}$ |
分析 利用球的对称性可知∠OEC=60°,利用等边三角形的性质,即可求出OE.
解答 解: 过球心O作OO′⊥平面BCD,则O′为等边三角形BCD的中心,
过球心O作OO′⊥平面BCD,则O′为等边三角形BCD的中心,
∵四边形ABCD是菱形,A=60°,
∴△BCD是等边三角形,
∵∠PEC=120°,
∴∠OEC=60°;
∵AB=2$\sqrt{3}$,
∴CE=3,
∴EO′=1,CO′=2,
∴OE=2,
故选:B.
点评 本题考查了棱锥与外接球的关系,考查求OE长,找出∠OEC=60°是解题关键.

练习册系列答案
相关题目
12.已知不等式x2+ax+b<0的解集是{x|-1<x<2},则a+b等于( )
| A. | -3 | B. | 1 | C. | -1 | D. | 3 |
16.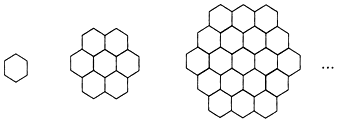 单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
 单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )
单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n幅图的蜂巢总数.则f(4)=________;f(n)=________( )| A. | 37 3n2-3n+1 | B. | 38 3n2-3n+2 | C. | 36 3n2-3n | D. | 35 3n2-3n-1 |
6.已知x,y满足$\left\{\begin{array}{l}y≥-1\\ x+y≤1\\ y≤x\end{array}\right.$,则z=2x+y的最小值是( )
| A. | -3 | B. | 1 | C. | $\frac{3}{2}$ | D. | 3 |
10.已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则关于函数y=f(x),下列说法正确的是( )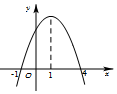
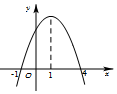
| A. | 在x=-1处取得极大值 | B. | 在区间[-1,4]上是增函数 | ||
| C. | 在x=1处取得极大值 | D. | 在区间[1,+∞)上是减函数 |
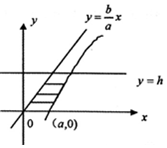 我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.