题目内容
19.若(1+2x)6=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6,则a0+a1+a3+a5=( )| A. | 364 | B. | 365 | C. | 728 | D. | 730 |
分析 分别取x=1、-1,0求出代数式的值,然后相加减计算即可得解.
解答 解:令x=1时,则36=a0+a1+a2+a3+a4+a5+a6=729,
令x=-1时,则(-1)6=a0-a1+a2-a3+a4-a5+a6=1,
令x=0时,a0=1
∴2(a1+a3+a5)=728,
∴a1+a3+a5=364
∴a0+a1+a3+a5=365
故选:D.
点评 本题考查了代数式求值,根据系数特点x取三个特殊值并求出系数的和是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.已知函数y=f(x)的导函数y=f′(x)的图象如图所示,则关于函数y=f(x),下列说法正确的是( )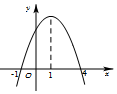
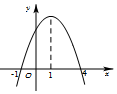
| A. | 在x=-1处取得极大值 | B. | 在区间[-1,4]上是增函数 | ||
| C. | 在x=1处取得极大值 | D. | 在区间[1,+∞)上是减函数 |
7.为了加强某站的安全检查,从甲乙丙等5名候选民警中选2名作为安保人员,则甲乙丙中有2人被选中的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{1}{10}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{20}$ |
4.在区间(0,+∞)内,函数f(x)=ex-x是( )
| A. | 增函数 | B. | 减函数 | C. | 先增后减 | D. | 先减后增 |
8.一动圆P与圆A:(x+1)2+y2=1外切,而与圆B:(x-1)2+y2=r2(r>3或0<r<1)内切,那么动圆的圆心P的轨迹是( )
| A. | 椭圆 | B. | 双曲线 | ||
| C. | 椭圆或双曲线一支 | D. | 抛物线 |
9.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区 5 户家庭,得到如下统计数据表:
根据上表可得回归直线方程 $\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,其中 $\widehat{b}$=0.76,$\widehat{a}$=y-$\widehat{b}$x,据此估计,该社区一户收入为 14 万元家庭年支出为( )
| 收入 x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出 y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.04 万元 | B. | 11.08 万元 | C. | 12.12 万元 | D. | 12.02 万元 |
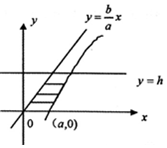 我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.
我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等高的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0),与x轴,直线y=h(h>0)及渐近线y=$\frac{b}{a}$x所围成的阴影部分(如图)绕y轴旋转一周所得的几何体的体积a2hπ.