题目内容
对于定义域为R的函数f(x),给出下列命题:
①若函数f(x)满足条件f(x-1)+f(1-x)=2,则函数f(x)的图象关于点(0,1)对称;
②若函数f(x)满足条件f(x-1)=f(1-x),则函数f(x)的图象关于y轴对称;
③在同一坐标系中,函数y=f(x-1)与y=f(1-x)其图象关于直线x=1对称;
④在同一坐标系中,函数y=f(1+x)与y=f(1-x)其图象关于y轴对称.
其中,真命题的序号是 .
①若函数f(x)满足条件f(x-1)+f(1-x)=2,则函数f(x)的图象关于点(0,1)对称;
②若函数f(x)满足条件f(x-1)=f(1-x),则函数f(x)的图象关于y轴对称;
③在同一坐标系中,函数y=f(x-1)与y=f(1-x)其图象关于直线x=1对称;
④在同一坐标系中,函数y=f(1+x)与y=f(1-x)其图象关于y轴对称.
其中,真命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:①取点(x,f(x)),则关于点(0,1)对称点的坐标为(-x,2-f(x)),利用条件可得结论;
②令t=1-x,有f(t)=f(-t),则函数y=f(x)的图象关于直线y轴对称;
③f(x)与y=f(-x)的图象关于直线x=0对称,利用图象的变换,可得结论;
④在同一坐标系中,点(x,y)在函数y=f(1+x)的图象上,则(-x,y)在y=f(1-x)的图象上.
②令t=1-x,有f(t)=f(-t),则函数y=f(x)的图象关于直线y轴对称;
③f(x)与y=f(-x)的图象关于直线x=0对称,利用图象的变换,可得结论;
④在同一坐标系中,点(x,y)在函数y=f(1+x)的图象上,则(-x,y)在y=f(1-x)的图象上.
解答:
解:①取点(x,f(x)),则关于点(0,1)对称点的坐标为(-x,2-f(x)),
∴2-f(x)=f(-x),
∵f(x-1)+f(1-x)=2,∴f(x)+f(-x)=2,
∴2-f(x)=f(-x),即①正确;
②若f(1-x)=f(x-1),令t=1-x,有f(t)=f(-t),
则函数y=f(x)的图象关于直线y轴对称,即②正确;
③∵f(x)与y=f(-x)的图象关于直线x=0对称,
函数y=f(x-1)与y=f(1-x)的图象可以由f(x)与y=f(-x)的图象向右移了一个单位而得到,
从而可得函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称,即③正确;
④在同一坐标系中,点(x,y)在函数y=f(1+x)的图象上,
则(-x,y)在y=f(1-x)的图象上,
∴函数y=f(1+x)与y=f(1-x)的图象关于y轴对称,即④正确.
综上,①②③④均为真命题.
故答案为:①②③④.
∴2-f(x)=f(-x),
∵f(x-1)+f(1-x)=2,∴f(x)+f(-x)=2,
∴2-f(x)=f(-x),即①正确;
②若f(1-x)=f(x-1),令t=1-x,有f(t)=f(-t),
则函数y=f(x)的图象关于直线y轴对称,即②正确;
③∵f(x)与y=f(-x)的图象关于直线x=0对称,
函数y=f(x-1)与y=f(1-x)的图象可以由f(x)与y=f(-x)的图象向右移了一个单位而得到,
从而可得函数y=f(x-1)与y=f(1-x)的图象关于直线x=1对称,即③正确;
④在同一坐标系中,点(x,y)在函数y=f(1+x)的图象上,
则(-x,y)在y=f(1-x)的图象上,
∴函数y=f(1+x)与y=f(1-x)的图象关于y轴对称,即④正确.
综上,①②③④均为真命题.
故答案为:①②③④.
点评:本题考查命题真假的判断,考查学生对抽象函数函数性质的理解与应用,是中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
用0到9这10个数字,可以组成没有重复数字且被5整除的三位数有( )
| A、72个 | B、136个 |
| C、200个 | D、648个 |
已知直线l:y=kx+1,椭圆
+
=1,则直线l与椭圆C的位置关系是( )
| x2 |
| 25 |
| y2 |
| 9 |
| A、相交 | B、相切 |
| C、相离 | D、三种位置关系都有可 |
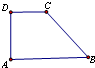 如图,长沙梅溪湖有一块梯形湖面,AB、AD是两条互相垂直的环湖面的公路,CD、CB是两条环湖面的游览小道,且AB=200m,AD=CD=100m.现在A处有一夹角为
如图,长沙梅溪湖有一块梯形湖面,AB、AD是两条互相垂直的环湖面的公路,CD、CB是两条环湖面的游览小道,且AB=200m,AD=CD=100m.现在A处有一夹角为