题目内容
已知圆C:x2+(y-1)2=5,直线L:mx-y+1-m=0.
①求证:对m∈R,直线L与圆C总有两个不同的交点;
②求直线L中,截圆所得的弦最长及最短时的直线方程.
①求证:对m∈R,直线L与圆C总有两个不同的交点;
②求直线L中,截圆所得的弦最长及最短时的直线方程.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:①将直线l的方程变形提出m,根据直线方程的斜截式,求出直线恒过点(1,1),即可证明结论;
②直线l截圆所得的弦最长时,一定过圆心;当弦长最短时,AC和直线L垂直,即可求得L的直线方程.
②直线l截圆所得的弦最长时,一定过圆心;当弦长最短时,AC和直线L垂直,即可求得L的直线方程.
解答:
①证明:∵直线L:mx-y+1-m=0即为y=m(x-1)+1,
∴直线l恒过(1,1),
∵12+(1-1)2=1<5,
∴A(1,1)在圆C:x2+(y-1)2=5的内部,
∴对m∈R,直线L与圆C总有两个不同的交点;
②解:被圆截得的弦最长的直线一定过圆心,方程为y=1,
它的圆心为C(0,1),由弦长最短,可得AC和直线L垂直,
故直线l的方程为x=1.
∴直线l恒过(1,1),
∵12+(1-1)2=1<5,
∴A(1,1)在圆C:x2+(y-1)2=5的内部,
∴对m∈R,直线L与圆C总有两个不同的交点;
②解:被圆截得的弦最长的直线一定过圆心,方程为y=1,
它的圆心为C(0,1),由弦长最短,可得AC和直线L垂直,
故直线l的方程为x=1.
点评:判断直线与圆的位置关系,一般利用圆心与直线的距离与半径的大小关系加以判断,有时也可转化为直线恒过的点来判断.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
某校从高一年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示: 某海轮以30n mile/h的速度航行,在A点测得海面上油井P在南偏东60°方向,向北航行40min后到达B点,测得油井P在南偏东30°方向,海轮改为北偏东60°的航向再行驶80min到达C点,求P、C间的距离.
某海轮以30n mile/h的速度航行,在A点测得海面上油井P在南偏东60°方向,向北航行40min后到达B点,测得油井P在南偏东30°方向,海轮改为北偏东60°的航向再行驶80min到达C点,求P、C间的距离.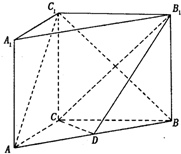 如图,AA1∥BB1∥CC1,AA1=BB1=CC1,AA1⊥面ABC且AC=3,BC=4,AB=5,AA1=4,点D为 AB的中点.
如图,AA1∥BB1∥CC1,AA1=BB1=CC1,AA1⊥面ABC且AC=3,BC=4,AB=5,AA1=4,点D为 AB的中点.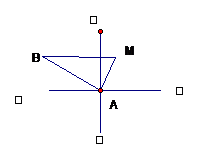 一艘轮船按照北偏西50°的方向,以15海里每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上,经过40分钟,轮船与灯塔的距离是5
一艘轮船按照北偏西50°的方向,以15海里每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上,经过40分钟,轮船与灯塔的距离是5