题目内容
称满足以下两个条件的有穷数列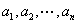 为
为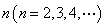 阶“期待数列”:
阶“期待数列”:
①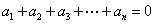 ;②
;②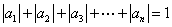 .
.
(1)若等比数列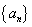 为
为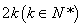 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及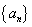 的通项公式;
的通项公式;
(2)若一个等差数列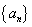 既是
既是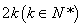 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列”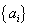 的前k项和为
的前k项和为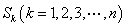 :
:
(i)求证: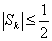 ;
;
(ii)若存在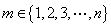 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
(1)①若 ,由①得,
,由①得, ,得
,得 ,矛盾.-----------1分
,矛盾.-----------1分
若 ,则由①
,则由①
 =0,得
=0,得 ,-------------3分
,-------------3分
由②得 或
或 .
.
所以, .数列
.数列 的通项公式是
的通项公式是
或 ------------------------------------4分
------------------------------------4分


记数列
 的前
的前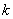 项和为
项和为 ,
,
则由(i)知, ,
,
 ,而
,而 ,
,
 ,从而
,从而 ,
, ,
,
又 ,
,
则 ,-------------------------16分
,-------------------------16分
 ,
,
 与
与
 不能同时成立,
不能同时成立,
所以,对于有穷数列 ,若存在
,若存在 使
使 ,则数列
,则数列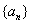 的和数列
的和数列
 不能为
不能为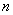 阶“期待数列”. ----------------------18分
阶“期待数列”. ----------------------18分

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 中,角A,B,C的对边分别为
中,角A,B,C的对边分别为 若
若 ,则角B的值为
,则角B的值为 B.
B.  C.
C.  D.
D. 
 的前
的前 (
( ),则
),则 的值是__________.
的值是__________. 是各项均为正数的等比数列,且
是各项均为正数的等比数列,且 与
与 的等比中项为2,则
的等比中项为2,则 的最小值等于 .
的最小值等于 . ,记
,记 ,若
,若 的取值范围是______________.
的取值范围是______________.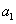 为整数;②对于任意的正整数
为整数;②对于任意的正整数 为偶数时,
为偶数时,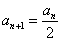 ;当
;当 .
. 成等差数列,求
成等差数列,求 (
( 且
且 N),数列
N),数列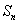 ,求证:
,求证: ;
; (
( N)时,都有
N)时,都有 .
. 的一条渐近线与直线2x+y-3=0垂直,则双曲线的离心率是
的一条渐近线与直线2x+y-3=0垂直,则双曲线的离心率是 B.
B. C.
C. D.
D.
 P为 圆上一点,求
P为 圆上一点,求 的最大值。
的最大值。 ,
,  随机取自集合
随机取自集合 ,则直线
,则直线 与圆
与圆 有公共点的概率是 .
有公共点的概率是 .