题目内容
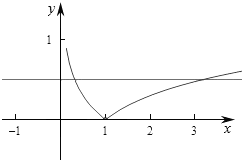
2.已知函数f(x)=|lnx|,a>b>0,f(a)=f(b),则$\frac{{{a^2}+{b^2}}}{a-b}$的最小值等于2$\sqrt{2}$.分析 根据对数函数的性质,求出ab=1,然后利用基本不等式求$\frac{{{a^2}+{b^2}}}{a-b}$的最小值.
解答 解:因为f(x)=|lnx|,f(a)=f(b),所以|lna|=|lnb|,
即lna=±lnb,又a>b>0,所以lna=-lnb,ab=1,
则$\frac{{{a^2}+{b^2}}}{a-b}$=$\frac{(a-b)^{2}+2ab}{a-b}=(a-b)+\frac{2}{a-b}≥2\sqrt{2}$,
当且仅当ab=1且a-b=$\frac{2}{a-b}$时取等号,
 ∴$\frac{{{a^2}+{b^2}}}{a-b}$的最小值 为2$\sqrt{2}$.
∴$\frac{{{a^2}+{b^2}}}{a-b}$的最小值 为2$\sqrt{2}$.
故答案为:2$\sqrt{2}$.
点评 本题主要考查基本不等式的应用,利用对数函数的图象和性质求出ab=1是解决本题的关键,注意基本不等式成立的条件.属于中档题

练习册系列答案
相关题目
13.已知f(x)的定义域为(0,+∞),f′(x)为f(x)的导函数,且满足f(x)>-xf′(x),则不等式f(x+1)>(x-1)f(x2-1)的解集是( )
| A. | (1,2) | B. | (1,+∞) | C. | (0,2) | D. | (2,+∞) |
7.如果sinα•cosα<0,sinα•tanα>0,那么角$\frac{α}{2}$的终边在( )
| A. | 第一或第三象限 | B. | 第二或第四象限 | C. | 第一或第二象限 | D. | 第三或第四象限 |
14.在函数:①y=cos|x|②y=|sinx|③$y=cos(2x+\frac{π}{6})$④$y=tan(2x-\frac{π}{4})$中,最小正周期为π的所有函数为( )
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ③④ |
12.利用独立性检验来考虑两个分类变量X和Y是否有关系时,如果K2的观测值k≈4.62,那么在犯错误的概率不超过0.05的前提下认为“X和Y有关系”.
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |