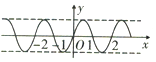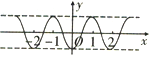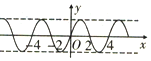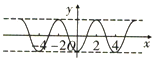题目内容
14.在函数:①y=cos|x|②y=|sinx|③$y=cos(2x+\frac{π}{6})$④$y=tan(2x-\frac{π}{4})$中,最小正周期为π的所有函数为( )| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ③④ |
分析 根据三角函数的图象与性质,分别求出四个函数的最小正周期即可.
解答 解:对于①,函数y=cos|x|的最小正周期为2π,不满足题意;
对于②,函数y=|sinx|的最小正周期为π,满足题意;
对于③,函数$y=cos(2x+\frac{π}{6})$的最小正周期为T=$\frac{2π}{2}$=π,满足题意;
对于④,函数$y=tan(2x-\frac{π}{4})$的最小正周期为T=$\frac{π}{2}$,不满足题意;
综上,最小正周期为π的函数是②③.
故选:C.
点评 本题考查了求三角函数的最小正周期的应用问题,是基础题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
5. 如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
 如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a1<a2 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
9.下列说法中正确的是( )
| A. | 第一象限角一定是正角 | B. | 终边与始边均相同的角一定相等 | ||
| C. | -834°是第四象限角 | D. | 钝角一定是第二象限角 |
19.某小区现有住房的面积为a平方米,在改造过程中政府决定每年拆除b平方米旧住房,同时按当店住房面积的10%建设新住房,则n年后该小区的住房面积为( )
| A. | a•1.1n-nb | B. | a•1.1n-10b(1.1n-1) | ||
| C. | n(1.1a-1) | D. | (a-b)1.1n |
4.在同一平面直角坐标系中,经过伸缩变换$\left\{\begin{array}{l}{x′=5x}\\{y′=3y}\end{array}\right.$后,曲线C变为曲线x′2+4y′2=1,则曲线C的方程为( )
| A. | 25x2+36y2=1 | B. | 9x2+100y2=1 | C. | 10x+24y=1 | D. | $\frac{2}{25}$x2+$\frac{8}{9}$y2=1 |