题目内容
13.已知f(x)的定义域为(0,+∞),f′(x)为f(x)的导函数,且满足f(x)>-xf′(x),则不等式f(x+1)>(x-1)f(x2-1)的解集是( )| A. | (1,2) | B. | (1,+∞) | C. | (0,2) | D. | (2,+∞) |
分析 根据函数的单调性得到x+1>x2-1>0,解不等式即可.
解答 解:∵f(x)>-xf′(x),
∴( x•f(x))′>0,故函数y=x•f(x)在(0,+∞)上是增函数,
由不等式f(x+1)>(x-1)f(x2-1)得:
(x+1)f(x+1)>(x+1)(x-1)f(x2-1),
即(x+1)f(x+1)>(x2-1)f(x2-1),
∴x+1>x2-1>0,解得:1<x<2,
故选:A.
点评 本题考查了函数的单调性问题,考查导数的应用以及转化思想,是一道中档题.

练习册系列答案
相关题目
5. 如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
 如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )
如图是某年青年歌手大奖赛中,七位评委为甲、乙两名选手打出的分数的茎叶图(其中m为数字0~9中的一个).去掉一个最高分和一个最低分后,甲、乙两名选手得分的平均数分别为a1,a2,则一定有( )| A. | a1>a2 | B. | a1<a2 | ||
| C. | a1=a2 | D. | a1,a2的大小与m的值有关 |
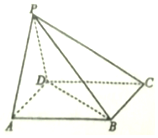 如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥平面ABCD.