题目内容
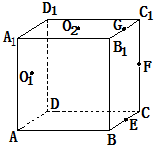 如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,Q1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点在同一个平面上的是
如图,正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,Q1、O2分别为四边形ADD1A1、A1B1C1D1的中心,则下列各组中的四个点在同一个平面上的是①A、C、O1、D1;②D、E、G、F;③A、E、F、D1=4;④G、E、O1、O2.
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:利用平面的基本性质和点在线上的方法解答.
解答:
解:正方体ABCD-A1B1C1D1中,若E、F、G分别为棱BC、C1C、B1C1的中点,Q1、O2分别为四边形ADD1A1、A1B1C1D1的中心,①所以O1是AD1的中点,所以O1是在平面ACD1;
②因为E、G、F在平面BCC1B1内,D不在平面BCC1B1内,所以D、E、G、F不共面;
③由已知可得EF∥AD1,所以A、E、F、D1共面;
④G、E、O1、O2.连接GO2,交A1D1于H,则H为A1D1的中点,连接HO1,则HO1∥GE,所以G、E、O1、O2.四点共面.
故答案为:①③④.
②因为E、G、F在平面BCC1B1内,D不在平面BCC1B1内,所以D、E、G、F不共面;
③由已知可得EF∥AD1,所以A、E、F、D1共面;
④G、E、O1、O2.连接GO2,交A1D1于H,则H为A1D1的中点,连接HO1,则HO1∥GE,所以G、E、O1、O2.四点共面.
故答案为:①③④.
点评:本题考查了平面的基本性质的运用来判断线共面以及点在平面内.

练习册系列答案
相关题目
下列函数中是奇函数是( )
A、y=x3-x+
| ||||||
B、y=
| ||||||
| C、y=x4-x2 | ||||||
| D、y=x6+x2+2 |
 在如图所示的图形上画一条直线,使下面的图形划为两个三角形.
在如图所示的图形上画一条直线,使下面的图形划为两个三角形.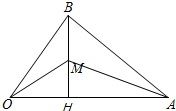
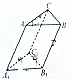 已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°.
已知斜三棱柱ABC-A1B1C1的底面是边长为4cm的正三角形,侧棱长为3cm,侧棱AA1与底面相邻两边都成60°. 已知椭圆E:
已知椭圆E: