题目内容
设an=(2n-1)•4n+1-(-1)n•n,求数列an的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:首先把数列分成两部分bn=(2n-1)4n+1和cn=(-1)n•n,对{bn}采用错位相加法求前n项和,对{cn}采用分类讨论求前n项和,通过运算求结果.
解答:
解:an=(2n-1)•4n+1-(-1)n•n,
故设:bn=(2n-1)4n+1数列{bn}的前n项和为Tn,
先求Tn=b1+b2+…+bn-1+bn=1•42+3•43+…+(2n-3)•4n+(2n-1)4n+14n+1 ①
4Tn=1•43+3•44+…+(2n-3)4n+1+(2n-1)4n+2 ②
①-②得:-3Tn=2(42+43+…+4n+1)-16-(2n-1)4n+2
解得:Tn=
设:cn=(-1)n•n,数列{cn}的前n项和为Kn,
当n为偶数时,Kn=
当n为奇数时,Kn=
-n
数列an的前n项和Sn=
故设:bn=(2n-1)4n+1数列{bn}的前n项和为Tn,
先求Tn=b1+b2+…+bn-1+bn=1•42+3•43+…+(2n-3)•4n+(2n-1)4n+14n+1 ①
4Tn=1•43+3•44+…+(2n-3)4n+1+(2n-1)4n+2 ②
①-②得:-3Tn=2(42+43+…+4n+1)-16-(2n-1)4n+2
解得:Tn=
| (32n-32)4n+80-4n+2 |
| 9 |
设:cn=(-1)n•n,数列{cn}的前n项和为Kn,
当n为偶数时,Kn=
| n |
| 2 |
当n为奇数时,Kn=
| n-1 |
| 2 |
数列an的前n项和Sn=
|
点评:本题考查的知识要点:数列的求和,错位相减法的应用,分类讨论思想在题中的应用及相关的运算问题.

练习册系列答案
相关题目
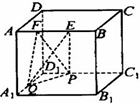 如图,在棱长为a的正方体ABCD-A1B1C1D1中,EF是棱AB上的一条线段,且EF=b<a,若Q是A1D1上的定点,P在C1D1上滑动,则四面体PQEF的体积( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,EF是棱AB上的一条线段,且EF=b<a,若Q是A1D1上的定点,P在C1D1上滑动,则四面体PQEF的体积( )| A、是变量且有最大值 |
| B、是变量且有最小值 |
| C、是变量无最大最小值 |
| D、是常量 |
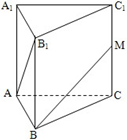 如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )
如图,已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是( )