题目内容
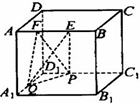如图，在棱长为a的正方体ABCD-A1B1C1D1中，EF是棱AB上的一条线段，且EF=b＜a，若Q是A1D1上的定点，P在C1D1上滑动，则四面体PQEF的体积（ ）| A、是变量且有最大值 |
| B、是变量且有最小值 |
| C、是变量无最大最小值 |
| D、是常量 |
考点：棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：根据等底同高的三角形面积相等及P到平面QEF的距离是定值，结合棱锥的体积公式，即可得出结论．
解答：
解：∵因为EF定长，Q到EF的距离就是Q到CD的距离也为定长，即底和高都是定值，
∴△QEF的面积是定值，
∵C1D1∥平面QEF，P在C1D1上滑动，
∴P到平面QEF的距离是定值．
即三棱锥的高也是定值，于是体积固定．
∴三棱锥P-QEF的体积是定值．
故选：D．
∴△QEF的面积是定值，
∵C1D1∥平面QEF，P在C1D1上滑动，
∴P到平面QEF的距离是定值．
即三棱锥的高也是定值，于是体积固定．
∴三棱锥P-QEF的体积是定值．
故选：D．
点评：本题考查的知识点棱锥的体积及点到平面的距离，其中线面平行时直线上到点到平面的距离相等是解答本题的关键．
练习册系列答案
相关题目
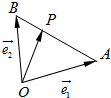设| OA |
| e1 |
| OB |
| e2 |
| e1 |
| e2 |
| OP |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|