题目内容
20.已知向量$\overrightarrow a$=(1,-2),$\overrightarrow b$=(1,1),$\overrightarrow m$=$\overrightarrow a$-$\overrightarrow b$,$\overrightarrow n$=$\overrightarrow a$+λ$\overrightarrow b$,如果$\overrightarrow m$⊥$\overrightarrow n$,那么实数λ=( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 先利用平面向量坐标运算法则求出$\overrightarrow{m}$,$\overrightarrow{n}$,再由$\overrightarrow m$⊥$\overrightarrow n$,利用向量垂直的条件能求出实数λ.
解答 解:∵向量$\overrightarrow a$=(1,-2),$\overrightarrow b$=(1,1),$\overrightarrow m$=$\overrightarrow a$-$\overrightarrow b$,$\overrightarrow n$=$\overrightarrow a$+λ$\overrightarrow b$,
∴$\overrightarrow{m}$=(0,-3),$\overrightarrow{n}$=(1+λ,-2+λ),
∵$\overrightarrow m$⊥$\overrightarrow n$,
∴$\overrightarrow{m}•\overrightarrow{n}$=0-3(-2+λ)=0,
解得λ=2.
故选:C.
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意向量垂直的性质的合理运用.

练习册系列答案
相关题目
5.设全集U=R,A={x|x2-x-6<0},B={x|y=lg(x+1)},则图中阴影部分表示的集合为( )
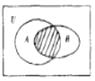

| A. | {x|-3<x<-1} | B. | {x|-3<x<0} | C. | {x|-1<x<3} | D. | {x|x>-1} |
2.若$\overrightarrow{a}$,$\overrightarrow{b}$不共线,且λ$\overrightarrow{a}$+μ$\overrightarrow{b}$=$\overrightarrow{0}$(λ,μ∈R),则( )
| A. | $\overrightarrow{a}$=$\overrightarrow{0}$,$\overrightarrow{b}$=$\overrightarrow{0}$ | B. | λ=μ=0 | C. | λ=0,$\overrightarrow{b}$=$\overrightarrow{0}$ | D. | $\overrightarrow{a}$=$\overrightarrow{0}$,μ=0 |