题目内容

5．设全集U=R，A={x|x2-x-6＜0}，B={x|y=lg（x+1）}，则图中阴影部分表示的集合为（　　）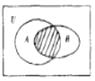
A．{x|-3＜x＜-1}B．{x|-3＜x＜0}C．{x|-1＜x＜3}D．{x|x＞-1}

分析 阴影部分表示的集合为A∩B，解出A，B，再求交集．

解答 解：阴影部分表示的集合为A∩B，而A={x|x2-x-6＜0}={x|-2＜x＜3}，B={x|y=lg（x+1）}={x|x＞-1}，
故A∩B={x|-1＜x＜3}，
故选C．

点评 本题考查了求Venn图表示的集合，关键是根据图形会判断出阴影部分表示的集合元素特征，再通过集合运算求出．

练习册系列答案
相关题目
15．在△ABC中，已知cosC+（cosA-$\sqrt{3}$sinA）cosB=0．
（1）求角B的大小；
（2）若sin（A-$\frac{π}{3}$）=$\frac{3}{5}$，求sin2C．
16．已知集合A={x|x2-9＞0}，B={x|2＜x≤5}，则A∩B=（　　）
A．（3，5]B．（-∞，-3）∪（5，+∞）C．（-∞，-3）∪[5，+∞）D．（-∞，2]∪（3，+∞）
13．中国传统文化中很多内容体现了数学的对称美，如图所示的太极图是由黑白两个鱼形纹组成的圆形图案，充分展现了相互转化、对称统一的形式美、和谐美，给出定义：能够将圆O的周长和面积同时平分的函数称为这个圆的“优美函数”，给出下列命题：
①对于任意一个圆O，其“优美函数“有无数个”；
②函数$f（x）=ln（{{x^2}+\sqrt{{x^2}+1}}）$可以是某个圆的“优美函数”；
③正弦函数y=sinx可以同时是无数个圆的“优美函数”；
④函数y=f（x）是“优美函数”的充要条件为函数y=f（x）的图象是中心对称图形．
其中正确的命题是（　　）
A．①③B．①③④C．②③D．①④
20．已知向量$\overrightarrow a$=（1，-2），$\overrightarrow b$=（1，1），$\overrightarrow m$=$\overrightarrow a$-$\overrightarrow b$，$\overrightarrow n$=$\overrightarrow a$+λ$\overrightarrow b$，如果$\overrightarrow m$⊥$\overrightarrow n$，那么实数λ=（　　）
A．4B．3C．2D．1
10．已知函数f（x）=$\left\{\begin{array}{l}{lo{g}_{a}（2-x），x≤1}\\{2|x-5|-2，3≤x≤7}\end{array}\right.$（a＞0，a≠1）的图象上关于直线x=1对称的点有且仅有一对，则实数a的取值范围是（　　）
A．[$\frac{\sqrt{7}}{7}$，$\frac{\sqrt{5}}{5}$]∪{$\sqrt{3}$}B．[$\sqrt{3}$，$\sqrt{5}$）∪{$\frac{\sqrt{7}}{7}$}C．[$\frac{\sqrt{7}}{7}$，$\frac{\sqrt{5}}{5}$]∪{$\sqrt{5}$}D．[$\sqrt{3}$，$\sqrt{7}$）∪{$\frac{\sqrt{5}}{5}$}
17．设a＞0且a≠1，b＞0，若函数y=ax+b的大致图象如图所示，则函数y=logax-b的图象为（　　）
A．B．C．D．
7．已知集合A={x|2x≥16}，B={x|log2x≥a}．
（1）当a=1时，求A∩B；
（2）若A是B的子集，求实数a的取值范围．
8．设a为实数，函数f（x）=ex-x+a，x∈R．
（1）求f（x）在区间[-1，2]上的最值；
（2）求证：当a＞-1，且x＞0时，${e^x}＞\frac{1}{2}{x^2}-ax+1$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网