题目内容
12.若实数x,y满足不等式组$\left\{\begin{array}{l}x≤2\\ y<1\\ x+2y-2≥0\end{array}\right.$,则$z=\frac{x+y+2}{x+1}$的取值范围是为[$\frac{4}{3}$,3).分析 作出不等式组对应的平面区域,利用z的几何意义,利用数形结合即可得到结论.
解答 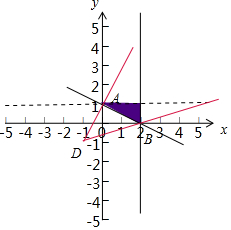 解:作出不等式组$\left\{\begin{array}{l}x≤2\\ y<1\\ x+2y-2≥0\end{array}\right.$对应的平面区域如图:
解:作出不等式组$\left\{\begin{array}{l}x≤2\\ y<1\\ x+2y-2≥0\end{array}\right.$对应的平面区域如图:
∵$z=\frac{x+y+2}{x+1}$=1+$\frac{y+1}{x+1}$,设k=$\frac{y+1}{x+1}$,则k的几何意义为区域内的点到定点D(-1,-1)的斜率,
由图象知BD的斜率最小,AD的斜率最大,如果A在可行域则k的最大为:$\frac{1+1}{0+1}$=2,最小为:$\frac{1+0}{2+1}$=$\frac{1}{3}$,
即$\frac{1}{3}≤$k<2,
则$\frac{4}{3}$≤k+1<3,
故$z=\frac{x+y+2}{x+1}$的取值范围是[$\frac{4}{3}$,3),
故答案为:[$\frac{4}{3}$,3).
点评 本题主要考查线性规划的应用,利用z的几何意义以及斜率的计算,通过数形结合是解决本题的关键.

练习册系列答案
相关题目
2.二项式(x-a)7的展开式中,含x4项的系数为-280,则${∫}_{a}^{2e}$$\frac{1}{x}$dx=( )
| A. | ln2 | B. | ln2+1 | C. | 1 | D. | $\frac{{{e^2}-1}}{{4{e^2}}}$ |
3.某变量x,y,z满足约束条件$\left\{\begin{array}{l}x+y≤2\\ 2x-3y≤9\\ x≥0\end{array}\right.$则z=3x-y的最大值为( )
| A. | -2 | B. | 10 | C. | 3 | D. | 9 |
7.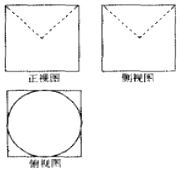 某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )
 某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )
某几何体的三视图如图所示,图中四边形都是边长为2的正方形,两条虚线相互垂直,则该几何体的表面积是( )| A. | $24+({\sqrt{2}+1})π$ | B. | $24+({\sqrt{2}-1})π$ | C. | $24-({\sqrt{2}+1})π$ | D. | $24-({\sqrt{2}-1})π$ |




