题目内容
1．
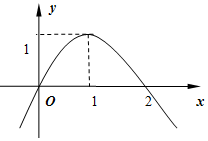已知函数f（x）=ax3+bx2+c过点（0，2），其导函数f'（x）的图象如图所示，则a+b+c=$\frac{8}{3}$．
分析 根据导函数的图象，可知0，2是方程3ax2+2bx=0的根，得到12a+4b=0，f′（1）=3a+2b=1，解得a，b的值，再根据函数f（x）=ax3+bx2+c过点（0，2），求出c的值．
解答 解：∵函数f（x）=ax3+bx2+c过点（0，2），
∴c=2，
∵f′（x）=3ax2+2bx，根据导函数的图象，
可知0，2是方程3ax2+2bx=0的根，
∴12a+4b=0，f′（1）=3a+2b=1，
解得a=-$\frac{1}{3}$，b=1，
∴a+b+c=-$\frac{1}{3}$+1+2=$\frac{8}{3}$，
故答案为：$\frac{8}{3}$．
点评 本题考查导函数的图象，导数值和函数值的求法，属于基础题．
练习册系列答案
相关题目
11．执行如图所示的程序框图，则输出的a值为（ ）
| A． | -3 | B． | $\frac{1}{3}$ | C． | -$\frac{1}{2}$ | D． | 2 |
16．若实数x，y满足条件$\left\{\begin{array}{l}{x-y+1≥0}\\{2x+y-2≥0}\\{x-1≤0}\end{array}\right.$则z=4x+3y的最小值为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
1．甲、乙两所学校高三年级分别有1200人，1000人，为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
（Ⅰ）计算x，y的值；
（Ⅱ）若规定考试成绩在[120，150]内为优秀，请分别估计两所学校数学成绩的优秀率；
（Ⅲ）根据以上统计数据完成2×2列联表，并判断是否有90%的把握认为两所学校的数学成绩有差异．
| 甲 校 | 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 3 | 4 | 8 | 15 | |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] | |
| 频数 | 15 | x | 3 | 2 |
| 乙 校 | 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 1 | 2 | 8 | 9 | |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] | |
| 频数 | 10 | 10 | y | 3 |
（Ⅱ）若规定考试成绩在[120，150]内为优秀，请分别估计两所学校数学成绩的优秀率；
（Ⅲ）根据以上统计数据完成2×2列联表，并判断是否有90%的把握认为两所学校的数学成绩有差异．
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |