题目内容
9.对于任意实数x,[x]表示不超过x的最大整数,如[-0,2]=-1,[1.72]=1,已知${a_n}=[{\frac{n}{3}}]({n∈{N^*}}),{S_n}$为数列{an}的前项和,则S2017=677712.分析 利用n∈N*,an=[$\frac{n}{3}$],可得S3n=3[0+1+2+…+(n-1)]+n=$\frac{3}{2}$n2-$\frac{n}{2}$,由2017=3×672+1,即可求得S2016,由a2017=672,S2017=S2016+a2017,即可求得S2017.
解答 解:∵n∈N*,an=[$\frac{n}{3}$],
∴n=3k,k∈N*时,a3k=k;
n=3k+1,k∈N时,a3k+1=k;
n=3k+2,k∈N时,a3k+2=k.
S3n=3[0+1+2+…+(n-1)]+n=3×$\frac{[1+(n+1)](n-1)}{2}$=$\frac{3}{2}$n2-$\frac{n}{2}$,
由2017=3×672+1,
∴S2016=S3×672=$\frac{3}{2}$×6722-$\frac{672}{2}$=677040,
a2017=672,
S2017=S2016+a2017=677040+672=677712,
故答案为:677712.
点评 本题主要考查数列与函数的综合运用,主要涉及了数列的推导与归纳,是新定义题,应熟悉定义,将问题转化为已知去解决,属于中档题.

练习册系列答案
相关题目
19.已知函数f(x)=|x+m|-|x+2|,若不等式f(x)+x≤0的解集为A,且[-1,1]⊆A,则实数m的取值范围为( )
| A. | (-1,1) | B. | [-1,1] | C. | (-1,1] | D. | [-1,1) |
20.集合M={x|x2<2x},N={x|log2(x-1)≤0},则M∩N=( )
| A. | (1,2) | B. | (1,2] | C. | [1,2) | D. | (0,2) |
17.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率等于$\frac{{\sqrt{5}}}{2}$,且点$({\sqrt{5},\frac{1}{2}})$在双曲线C上,则双曲线C的方程为( )
| A. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B. | ${y^2}-\frac{x^2}{4}=1$ | C. | $\frac{y^2}{4}-{x^2}=1$ | D. | $\frac{x^2}{4}-{y^2}=1$ |
4.若集合M={x∈N|x<6},N={x|x2-11x+18<0},则M∩N等于( )
| A. | {3,4,5} | B. | {x|2<x<6} | C. | {x|3≤x≤5} | D. | {2,3,4,5} |
14.若将函数$y=sin({2x+\frac{π}{3}})$的图象向右平移m(m>0)个单位长度,所得函数图象关于y轴对称,则m的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
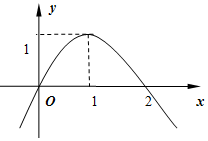 已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.
已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.