题目内容
1.甲、乙两所学校高三年级分别有1200人,1000人,为了了解两所学校全体高三年级学生在该地区六校联考的数学成绩情况,采用分层抽样方法从两所学校一共抽取了110名学生的数学成绩,并作出了频数分布统计表如下:| 甲 校 | 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 3 | 4 | 8 | 15 | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] | |
| 频数 | 15 | x | 3 | 2 |
| 乙 校 | 分组 | [70,80) | [80,90) | [90,100) | [100,110) |
| 频数 | 1 | 2 | 8 | 9 | |
| 分组 | [110,120) | [120,130) | [130,140) | [140,150] | |
| 频数 | 10 | 10 | y | 3 |
(Ⅱ)若规定考试成绩在[120,150]内为优秀,请分别估计两所学校数学成绩的优秀率;
(Ⅲ)根据以上统计数据完成2×2列联表,并判断是否有90%的把握认为两所学校的数学成绩有差异.
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
分析 (Ⅰ)由频数与总数关系可得x,y的值,先求出从甲、乙校各抽取的人数,再减去已知人数即得;
(Ⅱ)即求频率,按对应人数除以总数即可;
( III)按公式代入计算得k≈2.83>2.706,对照临界值表可知在犯错误的概率不超过0.10的前提下认为两个学校的数学成绩有差异.
解答 解:(Ⅰ)甲校抽取110×$\frac{1200}{2200}$=60人,乙校抽取110×$\frac{1000}{2200}$=50人,…(2分)
故x=10,y=7,…(4分)
(Ⅱ)估计甲校优秀率为$\frac{15}{60}$=25%,
乙校优秀率为$\frac{20}{50}$=40%.…(6分)
( III)表格填写如图,…(8分)
| 甲校 | 乙校 | 总计 | |
| 优秀 | 15 | 20 | 35 |
| 非优秀 | 45 | 30 | 75 |
| 总计 | 60 | 50 | 110 |
又因为1-0.10=0.9,故有90%的把握认为两个学校的数学成绩有差异.…(12分)
点评 本题主要考查独立性检验的应用,考查概率的计算,解题的关键是正确运算出观测值,理解临界值对应的概率的意义,属于中档题.

练习册系列答案
相关题目
20.集合M={x|x2<2x},N={x|log2(x-1)≤0},则M∩N=( )
| A. | (1,2) | B. | (1,2] | C. | [1,2) | D. | (0,2) |
16.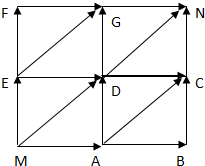 某商店老板设计了如下有奖游戏方案:顾客只要花10元钱,即可参加有奖游戏一次.游戏规则如下:棋子从点M开始沿箭头方向跳向N,每次只跳一步(即一个箭头),当下一步有方向选择时,跳的方法必须通过投掷骰子决定,方案如下:当掷出的点数为1时,沿$\overrightarrow{MD}$方向跳一步;当掷出的点数为2,4,6时,沿$\overrightarrow{ME}$方向跳一步;当掷出的点数为3,5时,沿$\overrightarrow{MA}$方向跳一步;奖励标准如表:
某商店老板设计了如下有奖游戏方案:顾客只要花10元钱,即可参加有奖游戏一次.游戏规则如下:棋子从点M开始沿箭头方向跳向N,每次只跳一步(即一个箭头),当下一步有方向选择时,跳的方法必须通过投掷骰子决定,方案如下:当掷出的点数为1时,沿$\overrightarrow{MD}$方向跳一步;当掷出的点数为2,4,6时,沿$\overrightarrow{ME}$方向跳一步;当掷出的点数为3,5时,沿$\overrightarrow{MA}$方向跳一步;奖励标准如表:
若该店平均每天有200人参加游戏,按每月30天计算.则该店开展此游戏每月获利的期望(均值)为2083元
(精确到1元)
 某商店老板设计了如下有奖游戏方案:顾客只要花10元钱,即可参加有奖游戏一次.游戏规则如下:棋子从点M开始沿箭头方向跳向N,每次只跳一步(即一个箭头),当下一步有方向选择时,跳的方法必须通过投掷骰子决定,方案如下:当掷出的点数为1时,沿$\overrightarrow{MD}$方向跳一步;当掷出的点数为2,4,6时,沿$\overrightarrow{ME}$方向跳一步;当掷出的点数为3,5时,沿$\overrightarrow{MA}$方向跳一步;奖励标准如表:
某商店老板设计了如下有奖游戏方案:顾客只要花10元钱,即可参加有奖游戏一次.游戏规则如下:棋子从点M开始沿箭头方向跳向N,每次只跳一步(即一个箭头),当下一步有方向选择时,跳的方法必须通过投掷骰子决定,方案如下:当掷出的点数为1时,沿$\overrightarrow{MD}$方向跳一步;当掷出的点数为2,4,6时,沿$\overrightarrow{ME}$方向跳一步;当掷出的点数为3,5时,沿$\overrightarrow{MA}$方向跳一步;奖励标准如表:| 从M到N用的步数 | 2 | 3 | 4 |
| 奖励金额(元) | 100 | 10 | 5 |
(精确到1元)
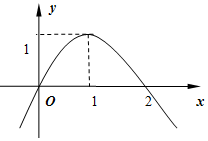 已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.
已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.