题目内容
2.已知函数f(x)=lnx+$\frac{a}{x}$-2.(1)求f(x)的单调性;
(2)若方程y=f(x)有两个根x1,x2(x1<x2),证明:x1+x2>2a.
分析 (1)求出函数的导数,通过讨论a的范围求出函数的单调区间,从而求出函数的最小值即可;
(2)求出函数的导数,从而确定0<x1<2a<x2,作f(2a-x1)-f(x2),利用换元法可证明f(2a-x1)-f(x2)<0,从而可得2a-x1<x2,从而得证.
解答 解:(1)f′(x)=$\frac{1}{x}$-$\frac{a}{x2}$=$\frac{x-a}{x2}$,(x>0)
所以当a≤0时,f′(x)>0,f(x)在(0,+∞)上单调递增;
当a>0时,f(x)在(0,a)上单调递减,在(a,+∞)上单调递增.…(5分)
(2)证明:若函数y=f(x)的两个零点为x1,x2(x1<x2),由(1)可得0<x1<a<x2.
令g(x)=f(x)-f(2a-x),(0<x<a)
则g′(x)=f′(x)+f′(2a-x)=(x-a)[$\frac{1}{x2}$-$\frac{1}{(2a-x)2}$]<0,
所以g(x)在(0,a)上单调递减,g(x)>g(a)=0,
即f(x)>f(2a-x).
令x=x1<a,则f(x1)>f(2a-x1),所以f(x2)=f(x1)>f(2a-x1),
由(1)可得f(x)在(a,+∞)上单调递增,所以x2>2a-x1,
故x1+x2>2a.…(12分)
点评 考查了导函数的应用,难点是函数的构造,难度较大.

练习册系列答案
相关题目
17.下列各组方程中,表示相同曲线的一组方程是( )
| A. | $y=\sqrt{x}$与y2=x | B. | y=x与$\frac{x}{y}=1$ | C. | y2-x2=0与|y|=|x| | D. | y=x0与y=1 |
14.已知函数f(x)=ax-x3,对区间(0,1)上的任意x1,x2,且x1<x2,都有f(x1)-f(x2)<x1-x2成立,则实数a的取值范围为( )
| A. | (0,1) | B. | [4,+∞) | C. | (0,4] | D. | (1,4] |
12.设复数z满足i3=z(1-i)(i为虚数单位),则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
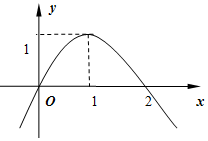 已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.
已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.