题目内容
6.已知函数f(x)=(sinx+cosx)2+2cos2x(x∈R).(Ⅰ)求函数f(x)的最大值及相应的x取值;
(Ⅱ)该函数的图象可以由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
分析 (Ⅰ)先根据二倍角公式、两角和的正弦公式进行化简,再由正弦函数的最值可确定答案.
(Ⅱ)由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:(Ⅰ)∵f(x)=(sinx+cosx)2+2cos2x=1+sin2x+cos2x+1=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+2,
∴当2x+$\frac{π}{4}$=2k$π+\frac{π}{2}$,即x=kπ+$\frac{π}{8}$,k∈Z时,函数f(x)的最大值为:2+2$\sqrt{2}$.
(Ⅱ)把y=sinx的图象向左平移$\frac{π}{4}$个单位,可得y=sin(x+$\frac{π}{4}$)的图象;
再把所得图象上的点的横坐标变为原来的$\frac{1}{2}$倍,可得y=sin(2x+$\frac{π}{4}$)的图象;
再把所得图象上的点的纵坐标变为原来的$\sqrt{2}$倍,可得y=$\sqrt{2}$sin(2x+$\frac{π}{4}$)的图象.
再把所得图象沿y轴向上平移2个单位,f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$)+2的图象.
点评 本题主要考查正弦函数的最值和二倍角公式、两角和的正弦公式的应用.考查对基础知识的简单综合应用.三角函数的公式比较多,要强化记忆.

练习册系列答案
相关题目
16.圆锥的母线长为L,过顶点的最大截面的面积为$\frac{1}{2}{L}^{2}$,则圆锥底面半径与母线长的比$\frac{r}{L}$的取值范围是( )
| A. | 0$<\frac{r}{L}<\frac{1}{2}$ | B. | $\frac{1}{2}≤\frac{r}{L}<1$ | C. | 0$<\frac{r}{L}<\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{2}}{2}≤\frac{r}{L}<1$ |
17.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率等于$\frac{{\sqrt{5}}}{2}$,且点$({\sqrt{5},\frac{1}{2}})$在双曲线C上,则双曲线C的方程为( )
| A. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B. | ${y^2}-\frac{x^2}{4}=1$ | C. | $\frac{y^2}{4}-{x^2}=1$ | D. | $\frac{x^2}{4}-{y^2}=1$ |
14.若将函数$y=sin({2x+\frac{π}{3}})$的图象向右平移m(m>0)个单位长度,所得函数图象关于y轴对称,则m的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{12}$ | D. | $\frac{7π}{12}$ |
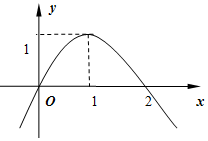 已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.
已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.