题目内容
12.在某次物理实验中,得到一组不全相等的数据x1,x2,x3,…,xn,若a是这组数据的“代表”,必须使$\sum_{i=1}^{n}$(xi-a)2最小,则a的值是$\frac{1}{n}$$\sum_{i=1}^{n}$xi.分析 有题意,利用加权平均数性质:(x1+x2+x3+…+xn)×$\frac{1}{n}$=$\overline{x}$.
解答 解:根据题意,由加权平均数性质可知:加权平均数表示“平均水平”,
即(x1+x2+x3+…+xn)×$\frac{1}{n}$=$\overline{x}$.
要使$\sum_{i=1}^{n}$(xi-a)2最小,即a=xi,
当xi等于加权平均数,即xi=$\frac{1}{n}$$\sum_{i=1}^{n}$xi时$\sum_{i=1}^{n}$(xi-a)2的值最小.
故答案为:$\frac{1}{n}$$\sum_{i=1}^{n}$xi.
点评 本题考察了加权平均数性质与不等式的相结合的运用,比较基础.

练习册系列答案
相关题目
2.设集合M={x|2x-x2≥0},N=$\{x|y=\frac{1}{{\sqrt{1-{x^2}}}}\}$,则M∩N等于( )
| A. | (-1,0] | B. | [-1,0] | C. | [0,1) | D. | [0,1] |
3.已知偶函数y=f(x)对于任意的x∈[0,$\frac{π}{2}$)满足f′(x)cosx+f(x)sinx>0,(其中f′(x)是函数f(x)的导函数),则下列不等式中成立的是( )
| A. | $\sqrt{2}$f(-$\frac{π}{3}$)<f($\frac{π}{4}$) | B. | $\sqrt{2}$f(-$\frac{π}{3}$)<f(-$\frac{π}{4}$) | C. | f(0)$>\sqrt{2}$f(-$\frac{π}{4}$) | D. | f($\frac{π}{4}$)$<\sqrt{3}$f($\frac{π}{3}$) |
20.集合M={x|x2<2x},N={x|log2(x-1)≤0},则M∩N=( )
| A. | (1,2) | B. | (1,2] | C. | [1,2) | D. | (0,2) |
17.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1的离心率等于$\frac{{\sqrt{5}}}{2}$,且点$({\sqrt{5},\frac{1}{2}})$在双曲线C上,则双曲线C的方程为( )
| A. | $\frac{y^2}{16}-\frac{x^2}{4}=1$ | B. | ${y^2}-\frac{x^2}{4}=1$ | C. | $\frac{y^2}{4}-{x^2}=1$ | D. | $\frac{x^2}{4}-{y^2}=1$ |
4.若集合M={x∈N|x<6},N={x|x2-11x+18<0},则M∩N等于( )
| A. | {3,4,5} | B. | {x|2<x<6} | C. | {x|3≤x≤5} | D. | {2,3,4,5} |
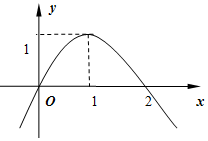 已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.
已知函数f(x)=ax3+bx2+c过点(0,2),其导函数f'(x)的图象如图所示,则a+b+c=$\frac{8}{3}$.