题目内容
在△ABC中,已知AB=1,BC=
,A=
,那么sinB= .
| 7 |
| 2π |
| 3 |
考点:正弦定理
专题:解三角形
分析:由余弦定理可得:a2=b2+c2-2bccosA,解得b.由正弦定理可得:
=
,即可得出.
| b |
| sinB |
| a |
| sinA |
解答:
解:由余弦定理可得:a2=b2+c2-2bccosA,
∴(
)2=b2+12-2bcos
,
化为b2+b-6=0,
解得b=2.
由正弦定理可得:
=
,
∴sinB=
=
=
.
故答案为:
.
∴(
| 7 |
| 2π |
| 3 |
化为b2+b-6=0,
解得b=2.
由正弦定理可得:
| b |
| sinB |
| a |
| sinA |
∴sinB=
| bsinA |
| a |
2×sin
| ||
|
| ||
| 7 |
故答案为:
| ||
| 7 |
点评:本题考查了利用正弦定理、余弦定理解三角形,考查了计算能力,属于基础题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知a、b∈R,直线l1:ax+2y+3=0和直线l2:x+by+2=0,则“ab=2”是“l1∥l2”的( )
| A、充分不必要条件. |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件. |
要得到函数y=sin(2x-
)的图象,应该把函数y=sin2x的图象( )
| π |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知直线l1:(m-1)x+y+2=0,l2:8x+(m+1)y+(m-1)=0,则“m=3”是“l1∥l2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
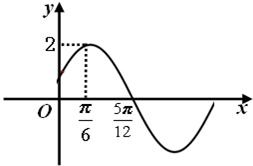 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<