题目内容
空间四点O（0，0，0），A（0，0，3），B（0，3，0），C（3，0，0），O点到平面ABC的距离为 ．
考点：点、线、面间的距离计算
专题：计算题,空间位置关系与距离
分析：由题意，O，A，B，C可看做正方体中的四个顶点，正方体的棱长为3，利用等体积，可求O点到平面ABC的距离．
解答：
解：由题意，O，A，B，C可看做正方体中的四个顶点，正方体的棱长为3，则△ABC的面积为
•(3
)2=
．
设O点到平面ABC的距离为d，则
•
•3•3•3=
•
•d，
解得d=
．
故答案为：
．
| ||
| 4 |
| 2 |
9
| ||
| 2 |
设O点到平面ABC的距离为d，则
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
9
| ||
| 2 |
解得d=
| 3 |
故答案为：
| 3 |
点评：将O，A，B，C可看做正方体中的四个顶点，利用等体积，是求O点到平面ABC的距离的关键．
练习册系列答案
相关题目
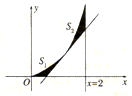已知l1为函数f（x）=x2（x∈[0，2]）在P（t，t2）（t∈（0，2））处的切线，l2为x=2，f（x），l1，l2与x轴所围成的图形如图所示．
在长方体ABCD-A1B1C1D1中，AB=BC=1，AA1=2，E为BB1中点．
如图，一个类似杨辉三角的数阵，则第n（n≥2）的第2个数为