题目内容
若α是第二象限的角,则角
所在的象限是( )
| α |
| 2 |
| A、第一象限 |
| B、第二象限 |
| C、第一象限或第二象限 |
| D、第一象限或第三象限 |
考点:象限角、轴线角
专题:三角函数的求值
分析:用不等式表示第二象限角α,再利用不等式的性质求出
满足的不等式,从而确定角
的终边在的象限.
| α |
| 2 |
| α |
| 2 |
解答:
解:∵α是第二象限角,
∴k•360°+90°<α<k•360°+180°,k∈Z,
则k•180°+45°<
<k•180°+90°,k∈Z,
令k=2n,n∈Z
有n•360°+45°<
<n•360°+90°,n∈Z;在一象限;
k=2n+1,n∈z,
有n•360°+225°<
<n•360°+270°,n∈Z;在三象限;
故选:D.
∴k•360°+90°<α<k•360°+180°,k∈Z,
则k•180°+45°<
| α |
| 2 |
令k=2n,n∈Z
有n•360°+45°<
| α |
| 2 |
k=2n+1,n∈z,
有n•360°+225°<
| α |
| 2 |
故选:D.
点评:本题考查象限角的表示方法,不等式性质的应用,通过角满足的不等式,判断角的终边所在的象限.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=3x-1(1≤x≤5)的图象是( )
| A、直线 | B、射线 |
| C、线段 | D、离散的点 |
下列函数中最小正周期为2π的函数是( )
A、y=sin(x-
| ||
B、y=cos(2x+
| ||
C、y=cos(3x-
| ||
D、y=tan(x-
|
已知
是非零向量,
≠
,则“
•
=
•
”是“
⊥(
-
)”成立的( )
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、非充分非必要条件 |
| D、充要条件 |
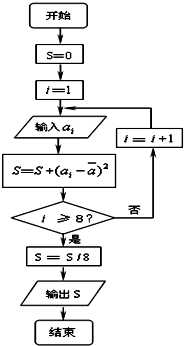 对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为
对一个作直线运动的质点的运动过程观测了8次,第i次观测得到的数据为ai,具体如表所示:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| ai | 40 | 41 | 43 | 43 | 44 | 46 | 47 | 48 |
. |
| a |
| A、5 | B、7 | C、40 | D、56 |
已知x、y均为正数,
+
=1,则xy有( )
| 2 |
| x |
| 8 |
| y |
| A、最大值64 | ||
B、最大值
| ||
| C、最小值64 | ||
D、最小值
|