题目内容
如图，在矩形ABCD中，AB=3，BC=4，点E、F分别在AB、BC边上，将△BEF沿EF折叠，点B落在B′处，当B′在矩形ABCD内部时，AB′的最小值为考点：解三角形的实际应用
专题：空间位置关系与距离
分析：根据翻折变换的性质，翻折前后图形图形大小不发生变化，以及当点B距点A的最小距离时，即AB′⊥EB′，A，B′，C在一条直线上，利用勾股定理，即可求出答案．
解答：
解：∵矩形ABCD纸片中，AD=4，CD=3，限定点E在边AB上，点F在边BC上，将△BEF沿EF翻折后叠合在一起，
∴当点B′距点A的最小距离时，∠B′EB要最大，则∠ECB′最小，而点F在边BC上，此时F点与点C重合，且B′在AC上时，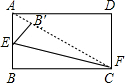
∵BC=B′C=4，∠EB′C=90°，
∴AC=
=5，
∴AB′=AC-B′C=5-4=1，
故答案为：1
∴当点B′距点A的最小距离时，∠B′EB要最大，则∠ECB′最小，而点F在边BC上，此时F点与点C重合，且B′在AC上时，
∵BC=B′C=4，∠EB′C=90°，
∴AC=
| AB2+BC2 |
∴AB′=AC-B′C=5-4=1，
故答案为：1
点评：此题主要考查了翻折变换，找出当点B距点A的最小距离时，B′点的位置是解决问题的关键．
练习册系列答案
相关题目
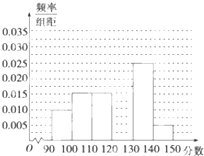某学校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六段[90，100），[100，110），…，[140，150）后得到如下部分频率分布直方图．观察图形的信息，回答下列问题：
