Question

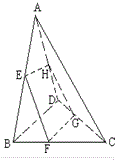如图，ABCD为空间四边形，点E、F分别是AB、BC的中点，点G、H分别在CD、AD上，且DH=

1

3

AD，DG=

1

3

CD，求证：直线EH、FG必相交于一点，且这个交点在直线BD上．

Answer 1

考点：平面的基本性质及推论

专题：空间位置关系与距离

分析：（1）根据已知中四边形ABCD是空间四边形，E，H分别是边AB，AD的中点，F，G分别是边CB，CD上的点，由平行线分线段成比例定理，我们易证明出EH∥FG，但EH≠FG，故四边形EFGH是梯形；
（2）由（1）的结论，我们易得EFGH四点共面，而且EF与FG相交，结合公理3我们易证明出FE和GH的交点在直线AC上．

解答： 证明：（1）∵E，F分别是边AB，BC的中点，∴EF∥AC，EF=

1

2

AC，
又∵DH=

1

3

AD，DG=

1

3

CD，∴HG∥AC，因此EF∥HG且EF≠HG
故四边形EFGH是梯形；（6分）
所以EH，FG相交，设EH∩FG=K
∵K∈EH，EH?平面ABD，
∴k∈平面ABD
同理K∈平面BCD，
又平面ABD∩平面BCD=BD
∴K∈BD
故EH和FG的交点在直线BD上．

点评：本题考查了平行线等分线段定理，及三线共点问题，其中利用平行线等分线段定理求出四边形EFGH的形状是解答本题的关键．