题目内容
已知圆M：x2+（y-1）2=1，圆N：x2+（y+1）2=1，直线l1，l2分别过圆心M，N，且l1与圆M相交于A，B，l2与圆N相交于C，D，P是椭圆
+
=1上的任意一动点，则
•
+
•
的最小值为 ．
| x2 |
| 3 |
| y2 |
| 4 |
| PA |
| PB |
| PC |
| PD |
考点：平面向量数量积的运算,圆与圆锥曲线的综合
专题：平面向量及应用,圆锥曲线的定义、性质与方程
分析：
=
+
，
=
-
，并且|
|=1，所以便可得到
•
=
2-1，同理可得到
•
=
2-1．所以
•
+
•
=
2+
2-2=(
+
)2-2
•
-2=14-2
•
≤14-2(
)2=6．
| PA |
| PM |
| MA |
| PB |
| PM |
| MA |
| MA |
| PA |
| PB |
| PM |
| PC |
| PD |
| PN |
| PA |
| PB |
| PC |
| PD |
| PM |
| PN |
| PM |
| PN |
| PM |
| PN |
| PM |
| PN |
|
| ||||
| 2 |
解答：
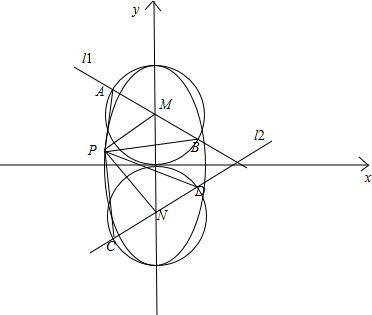6解：如图所示，
•
=(
+
)•(
+
)=(
+
)•(
-
)=
2-
2=
2-1；
同理，
•
=
2-1，P在椭圆上，所以|
|+|
|=4；
∴
•
+
•
=
2+
2-2=(|
|+|
)2-2|
||
|-2=14-2|
|
≥14-2(
)2=6；
∴
•
+
•
的最小值为6．
6解：如图所示，| PA |
| PB |
| PM |
| MA |
| PM |
| MB |
| PM |
| MA |
| PM |
| MA |
| PM |
| MA |
| PM |
同理，
| PC |
| PD |
| PN |
| PM |
| PN |
∴
| PA |
| PB |
| PC |
| PD |
| PM |
| PN |
| PM |
| PN| |
| PM |
| PN |
| PM| |
| PN| |
|
| ||||
| 2 |
∴
| PA |
| PB |
| PC |
| PD |
点评：考查向量的加法运算，相反向量，数量积的运算，以及椭圆的定义，基本不等式的运用．
练习册系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
复数z=
的实部是（ ）
| 1-i |
| i |
| A、-2 | B、-1 | C、1 | D、2 |
如图，ABCD为空间四边形，点E、F分别是AB、BC的中点，点G、H分别在CD、AD上，且DH=