题目内容
直线
(t为参数)的倾斜角为 .
|
考点:直线的参数方程
专题:直线与圆,坐标系和参数方程
分析:本题是直线的参数方程的普通形式,可以看出直线的倾斜角,也可以消去参数,通过直线的斜率求出直线的倾斜角,得到本题结论.
解答:
解:∵直线
(t为参数),
∴x-1=tcos50°,
y-2=tsn50°,
∴y-2=tan50°(x-1),
∴直线
(t为参数)的倾斜角为50°.
故答案为:50°.
|
∴x-1=tcos50°,
y-2=tsn50°,
∴y-2=tan50°(x-1),
∴直线
|
故答案为:50°.
点评:本题考查了直线的参数方程与倾斜角,本题难度不大,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知21×1=2,22×1×3=3×4,23×1×3×5=4×5×6,…,以此类推,第5个等式为( )
| A、24×1×3×5×7=5×6×7×8 |
| B、25×1×3×5×7×9=5×6×7×8×9 |
| C、24×1×3×5×7×9=6×7×8×9×10 |
| D、25×1×3×5×7×9=6×7×8×9×10 |
已知双曲线C:
-
=1(a>0,b>0),F是双曲线C的右焦点,点A是渐近线上第一象限内的一点,O为坐标原点,且|OA|=
,若
•
=
b2,则该双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| a2+b2 |
| OF |
| OA |
| 2 |
| 3 |
A、
| ||||
B、
| ||||
| C、2 | ||||
D、
|
若直线x-y+1=0与圆C:(x-a)2+y2=2有公共点,则实数a的取值范围是( )
| A、[-3,-1] |
| B、[-1,3] |
| C、[-3,1] |
| D、(-∞,-3]∪[1,+∞) |
已知圆C1:(x-2)2+(y-3)2=1.圆C2:(x-3)2+(y-4)2=16.M,N,分别是圆C1,C2上的动点.P为x轴上的动点,则|PM|+|PN|的最小值为( )
A、5
| ||
B、
| ||
C、6-2
| ||
D、
|
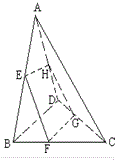 如图,ABCD为空间四边形,点E、F分别是AB、BC的中点,点G、H分别在CD、AD上,且DH=
如图,ABCD为空间四边形,点E、F分别是AB、BC的中点,点G、H分别在CD、AD上,且DH=