题目内容
下列命题中,正确的是( )
A、若|
| ||||||||||||||
B、若
| ||||||||||||||
C、若(
| ||||||||||||||
D、若
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由向量的模的概念和共线定理,即可判断A,B;由向量的平方即为模的平方,以及零向量的概念即可判断C;运用向量的数量积的定义和向量垂直的概念,即可判断D.
解答:
解:对于A.若|
|=|
|,则
,
不一定共线,则A错误;
对于B.若
,
共线,且
≠
,则存在唯一实数λ,使得
=λ
,则B错误;
对于C.若(
-
)2+(
-
)2=0,则(
-
)2=0且(
-
)2=0,即有
-
=
-
=
,则C正确;
对于D.若
•
=0,则|
|•|
|cos<
,
>=0,即有
2•
2=|
|2•|
|2不一定为0,则D错误.
故选C.
| a |
| b |
| a |
| b |
对于B.若
| a |
| b |
| b |
| 0 |
| a |
| b |
对于C.若(
| a |
| b |
| b |
| c |
| a |
| b |
| b |
| c |
| a |
| b |
| b |
| c |
| 0 |
对于D.若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
故选C.
点评:本题考查平面向量的有关知识:向量的模和向量共线定理、向量的数量积为0,注意区别实数范围的有关性质,运用向量的数量积的定义和模的定义是解题的关键.

练习册系列答案
相关题目
已知向量
,
均为单位向量,它们的夹角为600,实数x,y满足|x
+y
|=
,那么x+2y的最大值为( )
| a |
| b |
| a |
| b |
| 3 |
| A、3 | ||
B、
| ||
C、2
| ||
D、
|
已知m、n是三次函数f(x)=
x3+
ax2+2bx(a、b∈R)的两个极值点,且m∈(0,1),n∈(1,2),则
的取值范围是( )
| 1 |
| 3 |
| 1 |
| 2 |
| b+3 |
| a+2 |
A、(-∞,
| ||
B、(
| ||
| C、(-4,3) | ||
| D、(-∞,-4)∪(3,+∞) |
设向量
,
是夹角为
的单位向量,若
=3
,
=
-
,则向量
在
方向的投影为( )
| e1 |
| e2 |
| 2π |
| 3 |
| a |
| e1 |
| b |
| e1 |
| e2 |
| b |
| a |
A、
| ||
B、
| ||
C、-
| ||
| D、1 |
 如图,在直角梯形ABCD中,AD∥BC,BC⊥CD=4,已知AD=5,BC=4,CD=
如图,在直角梯形ABCD中,AD∥BC,BC⊥CD=4,已知AD=5,BC=4,CD=
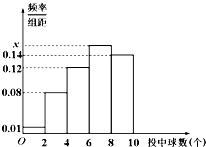 为鼓励中青年教师参加篮球运动,校工会组织了100名中青年教师进行投篮活动,每人投10次,投中情况绘成频率分布直方图(如图),则这100 名教师投中6至8个球的人数为
为鼓励中青年教师参加篮球运动,校工会组织了100名中青年教师进行投篮活动,每人投10次,投中情况绘成频率分布直方图(如图),则这100 名教师投中6至8个球的人数为