题目内容
设函数f（x）=
，点A0表示坐标原点，点An（n，f（n））（n∈N*）．若向量an=
+
+…+
，θn是an与i的夹角（其中i=（1，0）），则tanθn= ．
| 1 |
| x+1 |
| A0A1 |
| A1A2 |
| AN-1An |
考点：平面向量的综合题
专题：计算题,平面向量及应用
分析：利用向量的加法，结合函数解析式，即可得出结论．
解答：
解：∵向量an=
+
+…+
=
，点A0表示坐标原点，点An（n，f（n））（n∈N*）．
∴tanθn=
=
．
故答案为：
．
| A0A1 |
| A1A2 |
| An-1An |
| A0An |
∴tanθn=
| ||
| n |
| 1 |
| n(n+1) |
故答案为：
| 1 |
| n(n+1) |
点评：本题考查平面向量的综合，考查学生分析解决问题的能力，比较基础．
练习册系列答案
怎样学好牛津英语系列答案
相关题目
已知底面半径为1的一个圆锥的展开图是一个圆心角等于120°的扇形，则该圆锥的体积为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知△ABC面积为1，点P满足
=
+
，在△ABC内任取M，那么落入△BPC内的概率为（ ）
| AP |
| 1 |
| 5 |
| AB |
| 1 |
| 4 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
某人午觉醒来，发现表停了，他打开收音机，想听电台报时，他等待的时间不多于10分钟的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
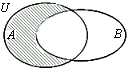已知全集U为实数集，集合A={x|x2-2x-3＜0}，B={x|y=ln（1-x）}，则图中阴影部分表示的集合为（ ）| A、{x|1≤x＜3} |
| B、{x|x＜3} |
| C、{x|x≤-1} |
| D、{x|-1＜x＜1} |
某班有50名学生，某次数学考试成绩平均分为70分，标准差为s；后来发现记录有误，甲同学得70分误记为40分，乙同学得50分误记为80分，更正后重新计算的标准差为S1，则S与S1的大小关系为（ ）
| A、S＞S1 |
| B、S＜S1 |
| C、S=S1 |
| D、不能确定 |