题目内容
已知△ABC面积为1,点P满足
=
+
,在△ABC内任取M,那么落入△BPC内的概率为( )
| AP |
| 1 |
| 5 |
| AB |
| 1 |
| 4 |
| AC |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:本题是概率的几何概型,研究的问题可以转化为△BPC与△ABC面积的比,利用
=
+
,得到点P的位置,再求出相应三角形的面积,得到本题结论.
| AP |
| 1 |
| 5 |
| AB |
| 1 |
| 4 |
| AC |
解答:
解:∵点P满足
=
+
,△ABC面积为1,
∴△APC的面积为:S1=
×AC×
hB-AC=
×1=
.
∴△APB的面积为:S2=
×AB×
hC-AB=
×1=
.
∴△PBC的面积为:1-
-
=
.
∴△PBC的面积与△ABC面积之比为:
.
∴在△ABC内任取M,那么落入△BPC内的概率为
.
故选D.
| AP |
| 1 |
| 5 |
| AB |
| 1 |
| 4 |
| AC |
∴△APC的面积为:S1=
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 5 |
∴△APB的面积为:S2=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
∴△PBC的面积为:1-
| 1 |
| 4 |
| 1 |
| 5 |
| 11 |
| 20 |
∴△PBC的面积与△ABC面积之比为:
| 11 |
| 20 |
∴在△ABC内任取M,那么落入△BPC内的概率为
| 11 |
| 20 |
故选D.
点评:本题考查了概率的几何概型,本题主要研究△BPC与△ABC面积的比,本题难度不大,属于基础题.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
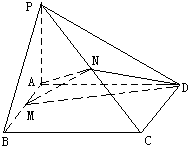 已知:ABCD是矩形,设PA=a,PA⊥平面ABCD,M,N分别是AB,PC的中心点.
已知:ABCD是矩形,设PA=a,PA⊥平面ABCD,M,N分别是AB,PC的中心点. 已知四面体O-ABC中,M、N分别是OA、BC的中点,P是MN上(靠近点M)的三等分点,其中OA=OB=OC=1,∠AOC=∠AOB=∠BOC=60°,求异面直线OP与AB所成角的余弦值.(用向量法)
已知四面体O-ABC中,M、N分别是OA、BC的中点,P是MN上(靠近点M)的三等分点,其中OA=OB=OC=1,∠AOC=∠AOB=∠BOC=60°,求异面直线OP与AB所成角的余弦值.(用向量法)