题目内容
9.下列函数中哪个与函数y=-x相等( )| A. | $y=-\sqrt{x^2}$ | B. | $y=\frac{-x(x-1)}{x-1}$ | ||
| C. | y=-logaax(a>0且a≠1) | D. | $y=-\sqrt{x}•\sqrt{x}$ |
分析 根据两个函数的定义域相同、对应关系也相同,即可判断它们是相等函数.
解答 解:对于A,函数y=-$\sqrt{{x}^{2}}$=-|x|(x∈R),与y=-x(x∈R)的对应关系不同,不是相等函数;
对于B,函数y=$\frac{-x(x-1)}{x-1}$=-x的定义域是{x|x≠0},与y=-x(x∈R)的定义域不同,不是相等函数;
对于C,函数y=-logaax=-x(x∈R),与y=-x(x∈R)的定义域相同,对应关系也相同,是相等函数;
对于D,函数y=-$\sqrt{x}$•$\sqrt{x}$=-x(x≥0),与y=-x(x∈R)定义域不同,不是相等函数.
故选:C.
点评 本题考查了函数的定义与应用问题,是基础题.

练习册系列答案
相关题目
19.设复数z1,z2在复平面内的对应点关于虚轴对称,若z1=1-2i,其中i是虚数单位,则$\frac{{z}_{2}}{{z}_{1}}$的虚部为( )
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$i | D. | $\frac{4}{5}$i |
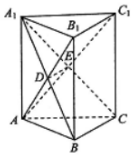 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,A1B与AB1交于点D,A1C与AC1交于点E.