题目内容

设向量
a
=（1，2），向量
b
=（-3，4），向量
c
=（3，2），则向量（
a
+2
b
）•
c
=（　　）
A、（-15，12）B、0
C、5D、-11
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：由向量的坐标运算可得
a
+2
b
的坐标，由数量积的坐标运算可得．
解答： 解：∵
a
=（1，2），
b
=（-3，4），
c
=（3，2），
∴
a
+2
b
=（1，2）+（-6，8）=（-5，10），
∴（
a
+2
b
）•
c
=-5×3+10×2=5
故选：C
点评：本题考查平面向量的数量积的坐标运算，属基础题．
练习册系列答案
相关题目
函数y=lg（sinx-cosx-1）的定义域为
 
．
已知圆O：x2+y2=4，过点M（1，
2
）的两条弦AC，BD互相垂直，则AC+BD的最大值是（　　）
A、6
B、2
10
C、4
3
D、5
2
对于正态分布的概率有这样几组已知参考数据：当X～N（μ，σ2），则P（μ-σ＜X≤μ+σ）=0.6826，P（μ-2σ＜X≤μ+2σ）=0.9544，P（μ-3σ＜X≤μ+3σ）=0.9974．
已知X～N（4，1），求P（5＜X＜6）的值．
如果程序框图的输出结果是6，那么在判断框中①表示的“条件”应该是（　　）
A、i≥3B、i≥4
C、i≥5D、i≥6
集合A={（x，y）|y=a}，集合B={（x，y）|y=bx+1，b＞0，b≠1}，若集合A∩B=ϕ，则实数a的取值范围是
 
．
集合A={a，b}，B={-1，0，1}，从A到B的映射f满足f（a）+f（b）=0，那么这样的映射f的个数有（　　）
A、2个B、3个C、5个D、8个
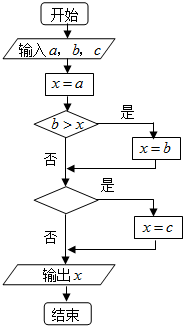如图的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（　　）
A、c＞xB、x＞a
C、c＞bD、b＞c
设集合U=R，集合A={x|x2-2x＞0}，则∁UA等于（　　）
A、{x|x＜0或x＞2}
B、{x|x≤0或x≥2}
C、{x|0＜x＜2}
D、{x|0≤x≤2}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网