题目内容
甲、乙二人各自选择中午12时到下午1时随机到达某地,他们约定:先到者等候15分钟后再离开,则他们能够会面的概率为 .
考点:几何概型
专题:概率与统计
分析:本题是一个几何概型,试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1},满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,|x-y|≤
},根据几何概型概率公式可得.
| 1 |
| 4 |
解答:
解:记甲、乙二人到达的时刻分别为x,y,
试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1}
事件对应的集合表示的面积(图中正方形)是S=1,
满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,|x-y|≤
},
事件对应的集合表示的面积(图中阴影)是1-2×
×
×
=
根据几何概型概率公式得到P=
故答案为:
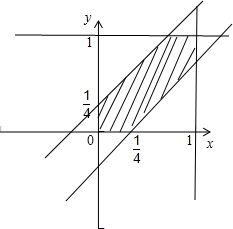
试验包含的所有事件是Ω={(x,y)|0≤x≤1,0≤y≤1}
事件对应的集合表示的面积(图中正方形)是S=1,
满足条件的事件是A={(x,y)|0≤x≤1,0≤y≤1,|x-y|≤
| 1 |
| 4 |
事件对应的集合表示的面积(图中阴影)是1-2×
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 16 |
根据几何概型概率公式得到P=
| 7 |
| 16 |
故答案为:
| 7 |
| 16 |

点评:本题考查几何概型,作图是解决问题的关键,属基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案
相关题目
方程5x-1•103x=8x的解集是( )
| A、{1,4} | ||
B、{
| ||
C、{1,
| ||
D、{4,
|
下面程序运行时,从键盘输入4,则输出结果为( )


| A、4 | B、8 | C、15 | D、2 |
 为了测算如图的阴影部分的面积,作一个边长为8的正方形将其包含在内,并向正方形内随机投掷800个黄豆,已知恰有300个落在阴影部分.据此,可估计阴影部分的面积为
为了测算如图的阴影部分的面积,作一个边长为8的正方形将其包含在内,并向正方形内随机投掷800个黄豆,已知恰有300个落在阴影部分.据此,可估计阴影部分的面积为