题目内容
设（2-x）5=a0+a1x+a2x2…+a5x5，那么
的值为（ ）
| a0+a2+a4 |
| a1+a3+a5 |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |
考点：二项式系数的性质
专题：二项式定理
分析：在所给的等式中，分别令x=1、x=-1可得到两个等式，由这两个等式解出a0+a2+a4 和a1+a3+a5 的值，可得
的值．
| a0+a2+a4 |
| a1+a3+a5 |
解答：
解：在（2-x）5=a0+a1x+a2x2…+a5x5中，
令x=1可得 a0+a1+a2+…+a5 =1 ①，令x=-1可得 a0-a1+a2-…-a5 =35 ②．
由①②求得 a0+a2+a4=122，a1+a3+a5 =-121，
∴
=-
，
故选：B．
令x=1可得 a0+a1+a2+…+a5 =1 ①，令x=-1可得 a0-a1+a2-…-a5 =35 ②．
由①②求得 a0+a2+a4=122，a1+a3+a5 =-121，
∴
| a0+a2+a4 |
| a1+a3+a5 |
| 122 |
| 121 |
故选：B．
点评：本题主要考查二项式定理的应用，注意根据题意，分析所给代数式的特点，通过给二项式的x赋值，求展开式的系数和，可以简便的求出答案，属于基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
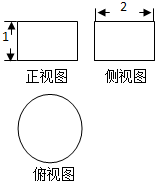如图所示，一个空间几何体的正视图和侧视图都是相邻两边的长分别为1和2的矩形，俯视图是一个圆，那么这个几何体的体积为（ ）| A、4π | ||
| B、π | ||
C、
| ||
D、
|
若θ∈[
，
]，sin2θ=
，则sinθ=（ ）
| π |
| 4 |
| π |
| 2 |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（
-2x2）5的展开式中常数项是（ ）
| 1 | ||
|
| A、-5 | B、5 | C、-10 | D、10 |
已知函数f（x）x∈（a，b）的导函数为f′（x），原命题为“若f′（x）＜0，则f（x）在（a，b）上单调递减”，关于其逆命题、否命题、逆否命题真假性的判断依次如下，正确的是（ ）
| A、真，真，真 |
| B、假，假，假 |
| C、真，真，假 |
| D、假，假，真 |
已知抛物线C1：x2=2y的焦点为F，以F为圆心的圆C2交C1于A，B两点，交C1的准线于C，D两点，若四边形ABCD是矩形，则圆C2的方程为（ ）
| A、x2+（y-1）2=12 | ||
| B、x2+（y-1）2=16 | ||
C、x2+（y-
| ||
D、x2+（y-
|
定义在R上的函数f（x）满足：对任意α，β∈R，总有f（α+β）-[f（α）+f（β）]=2014，则下列说法正确的是（ ）
| A、f（x）+1是奇函数 |
| B、f（x）-1是奇函数 |
| C、f（x）+2014是奇函数 |
| D、f（x）-2014是奇函数 |