题目内容

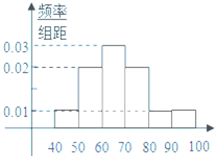某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生成绩进行统计，得到如图所示的样本频率分布直方图．若规定60分及以上为合格，则估计这1000名学生中合格人数是（　　）名．
A、400B、600
C、700D、800
考点：频率分布直方图
专题：概率与统计
分析：利用频率分布直方图先求出合格学生的频率，再求合格学生人数．
解答： 解：由频率分布直方图知：
这1000名学生中合格人数是：1000×[1-（0.01+0.02）×10]=700（人）．
故选：C．
点评：本题考查合格学生人数的求法，是基础题，解题时要认真审题，注意频率分布直方图的合理运用．
练习册系列答案
相关题目
如图，一个球形广告气球被一束入射角为30°的平行光线照射，其投影是一个最长的弦长为5米的椭圆，则制作这个广告气球至少需要的面料是
 
m2．
设a是实数，则“a=1”是“a2=1”的（　　）
A、充分而不必要条件
B、必要而不必要条件
C、充分必要条件
D、既不充分也不必要条件
（
1
x
-2x2）5的展开式中常数项是（　　）
A、-5B、5C、-10D、10
已知函数f（x）=（1-2x3）6，则f′（1）等于（　　）
A、0B、-6C、-36D、36
已知抛物线C1：x2=2y的焦点为F，以F为圆心的圆C2交C1于A，B两点，交C1的准线于C，D两点，若四边形ABCD是矩形，则圆C2的方程为（　　）
A、x2+（y-1）2=12
B、x2+（y-1）2=16
C、x2+（y-
1
2
）2=3
D、x2+（y-
1
2
）2=4
关于x的不等式x2-ax-6a2＜0（a＞0）的解集为（x1，x2），且x2-x1=10，则a=（　　）
A、2
B、5
C、
5
2
D、
3
2
若点O和点F分别为椭圆
x2
2
+y2=1的中心和左焦点，点P为椭圆上的任意一点，则
OP
•
FP
的最大值为（　　）
A、
2
+2
B、
2
-1
C、
2
+4
D、
2
+
3
2
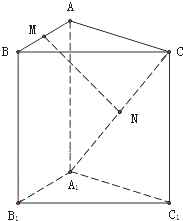在三棱柱ABC-A1B1C1中，M、N分别是AB、A1C的中点，求证：MN∥平面BCB1C1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网