题目内容
求y=
(x>-1)的最大值.
| x+1 |
| x2+3x+4 |
考点:基本不等式
专题:不等式的解法及应用
分析:由题意可得x+1>0,变形可得
=x+1+
+1,由基本不等式可得
的最小值为,进而由倒数关系可得y的最大值.
| 1 |
| y |
| 2 |
| x+1 |
| 1 |
| y |
解答:
解:∵x>-1,∴x+1>0,
∴
=
=
=x+1+
+1≥2
+1=2
+1
当且仅当x+1=
即x=
-1时取等号,
∴
的最小值为2
+1,
∴y=
(x>-1)的最大值为
=
∴
| 1 |
| y |
| x2+3x+4 |
| x+1 |
| (x+1)2+(x+1)+2 |
| x+1 |
=x+1+
| 2 |
| x+1 |
(x+1)
|
| 2 |
当且仅当x+1=
| 2 |
| x+1 |
| 2 |
∴
| 1 |
| y |
| 2 |
∴y=
| x+1 |
| x2+3x+4 |
| 1 | ||
2
|
2
| ||
| 7 |
点评:本题考查基本不等式求最值,正确变形是解决问题的关键,属基础题.

练习册系列答案
相关题目
若sin(180°+α)+cos(90°+α)=-a,则cos(270°-α)+2sin(360°-α)的值是( )
A、-
| ||
B、-
| ||
C、
| ||
D、
|
以点(1,0)为圆心,且过坐标原点的圆的方程为( )
| A、x2+y2+2x=0 |
| B、x2+y2+x=0 |
| C、x2+y2-x=0 |
| D、x2+y2-2x=0 |
如图,一个几何体的三视图如图所示,则该多面体的几条棱中,最长的棱的长度为( )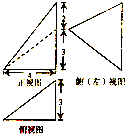

A、3
| ||
B、
| ||
C、
| ||
D、3
|
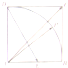 如图,正方形ABCD中,E为AB上一点,P为以点A为圆心,以AB为半径的圆弧上一点,若
如图,正方形ABCD中,E为AB上一点,P为以点A为圆心,以AB为半径的圆弧上一点,若