题目内容
4.设F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1(a>0,b>0)$的两个焦点,M,N是双曲线C的一条渐近线上的两点,四边形MF1NF2为矩形,A为双曲线的一个顶点,若△AMN的面积为$\frac{1}{2}{c}^{2}$,则该双曲线的离心率为( )| A. | 3 | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
分析 设M(x,$\frac{b}{a}$x),由题意,|MO|=c,则x=a,∴M(a,b),利用△AMN的面积为$\frac{1}{2}{c}^{2}$,建立方程,即可求出双曲线的离心率.
解答 解:设M(x,$\frac{b}{a}$x),由题意,|MO|=c,则x=a,∴M(a,b),
∵△AMN的面积为$\frac{1}{2}{c}^{2}$,
∴$\frac{1}{2}•a•b=\frac{1}{4}{c}^{2}$,
∴4a2(c2-a2)=c4,
∴e4-4e2+4=0,
∴e=$\sqrt{2}$.
故选D.
点评 本题考查双曲线的离心率,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.若复数z满足(1+i)z=i(i是虚数单位),则z的虚部为( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}i$ |
9.2016年下半年,锦阳市教体局举行了市教育系统直属单位职工篮球比赛,以增强直属单位间的交流与合作,组织方统计了来自A1,A2,A3,A4,A5等5个直属单位的男子篮球队的平均身高与本次比赛的平均得分,如表所示:
(1)根据表中数据,求y关于x的线性回归方程;(系数精确到0.01)
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
| 单位 | A1 | A2 | A3 | A4 | A5 |
| 平均身高x(单位:cm) | 170 | 174 | 176 | 181 | 179 |
| 平均得分y | 62 | 64 | 66 | 70 | 68 |
(2)若M队平均身高为185cm,根据(I)中所求得的回归方程,预测M队的平均得分(精确到0.01)
注:回归当初$\widehat{y}=\widehat{b}x+\widehat{a}$中斜率和截距最小二乘估计公式分别为$\widehat{b}=\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}=\overline{y}-\widehat{b}\overline{x}$.
16.“a=0”是“直线l1:ax+y-1=0与直线l2:x+ay-1=0垂直”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
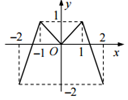 如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )
如图,定义在[-2,2]的偶函数f(x)的图象如图所示,函数g(x)=f(x)-$\frac{1}{4}x+\frac{1}{2}$的零点个数为( )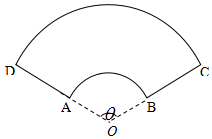 某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧$\widehat{AB}$、$\widehat{CD}$所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).