题目内容
已知函数f(x)=ax2-bx+1.
(Ⅰ)若f(x+1)-f(x)=2x,求a,b的值;
(Ⅱ)若b=a+2,且f(x)在(-2,-l)内恰有-个零点,求a的取值范围.
(Ⅰ)若f(x+1)-f(x)=2x,求a,b的值;
(Ⅱ)若b=a+2,且f(x)在(-2,-l)内恰有-个零点,求a的取值范围.
考点:函数的零点
专题:函数的性质及应用
分析:(1)f(x+1)-f(x)=2ax+a-b=2x,恒等式成立问题,列方程.(2)根据二次函数的零点判断,分a=0.a≠0,讨论.
解答:
解:(1)∵函数f(x)=ax2-bx+1.
f(x+1)-f(x)=2x,
∴f(x+1)-f(x)=2ax+a-b,
∴2x=2ax+a-b,
故a=1,b=1
(2)∵f(x)=ax2-bx+1,b=a+2,
∴f(x)=ax2-(a+2)x+1,
∵f(x)在(-2,-l)内恰有-个零点,
∴当a=0时,f(x)=-2x+1,零点为
∉(-2,-l)内,
当a≠0时,△=a2+4>0,对称轴x=
+
,
∴f(-2)f(-1)<0,
即(6a+5)(2a+3)<0
-
<a<-
,
故实数a的取值范围:-
<a<-
f(x+1)-f(x)=2x,
∴f(x+1)-f(x)=2ax+a-b,
∴2x=2ax+a-b,
故a=1,b=1
(2)∵f(x)=ax2-bx+1,b=a+2,
∴f(x)=ax2-(a+2)x+1,
∵f(x)在(-2,-l)内恰有-个零点,
∴当a=0时,f(x)=-2x+1,零点为
| 1 |
| 2 |
当a≠0时,△=a2+4>0,对称轴x=
| 1 |
| 2 |
| 1 |
| a |
∴f(-2)f(-1)<0,
即(6a+5)(2a+3)<0
-
| 3 |
| 2 |
| 5 |
| 6 |
故实数a的取值范围:-
| 3 |
| 2 |
| 5 |
| 6 |
点评:本题考查了函数的性质,化简运算,函数的零点判断问题,属于中档题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案
相关题目
已知直线l1:x+ay+6=0和l2:(a-2)x+3y+2a=0,则l1∥l2时,a的值为( )
| A、a=3,a=-1 |
| B、a=3 |
| C、a=-1 |
| D、以上都不对 |
如图是计算t=12×22×…×i2的程序,程序中循环体执行的次数为( )


| A、3 | B、4 | C、5 | D、6 |
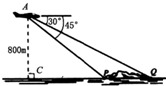 某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).
某次飞行表演中,一架直升从空中A处测出前下方海岛两侧海岸P、Q处的俯角分别是45°和30°(如右图所示,A、P、Q在同一平面内).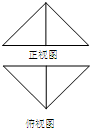 把边长为1的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图与俯视图均为全等的等腰直角三角形,如图所示,则侧视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,连结AC,得到三棱锥C-ABD,其正视图与俯视图均为全等的等腰直角三角形,如图所示,则侧视图的面积为( )