题目内容
14.(x2+2)(x-$\frac{1}{x}$)6的展开式中常数项为-25.分析 线求出(x-$\frac{1}{x}$)6展开式中的常数项与含$\frac{1}{{x}^{2}}$的系数,再求(x2+2)(x-$\frac{1}{x}$)6展开式中的常数项.
解答 解:(x-$\frac{1}{x}$)6展开式的通项公式为:
Tr+1=${C}_{6}^{r}$•x6-r•${(-\frac{1}{x})}^{r}$=(-1)r•${C}_{6}^{r}$•x6-2r,
令6-2r=0,解得r=3,
∴T3+1=(-1)3•${C}_{6}^{3}$=-20;
令6-2r=-2,解得r=4,
∴T4+1=(-1)4•${C}_{6}^{4}$•$\frac{1}{{x}^{2}}$=15•$\frac{1}{{x}^{2}}$;
∴(x2+2)(x-$\frac{1}{x}$)6展开式中常数项为:
2×(-20)+15=-25.
故答案为:-25.
点评 本题考查了利用二项展开式的通项公式求展开式中特定项的应用问题,熟练掌握二次项系数的特征是解题的关键

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.sin20°cos40°+sin70°sin140°的值等于( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
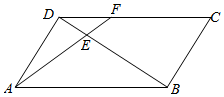 如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.
如图,点E是平行四边形ABCD对角线BD的4等分点中最靠近点D的那个分点,线段AE的延长线交CD于点F,若|$\overrightarrow{AB}$|=2,|$\overrightarrow{AD}$|=1,<$\overrightarrow{AB}$,$\overrightarrow{AD}$>=60°,则$\overrightarrow{AF}$•$\overrightarrow{AD}$的值为$\frac{4}{3}$.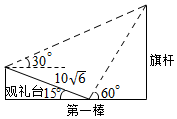 如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.
如图,在坡角(坡面与水平面的夹角)为15°的观礼台上,某一列座位与旗杆在同一个垂直于地面的平面上,在该列的第一排和最后一排测得旗杆的仰角分别为60°和30°,且第一排和最后一排的距离10$\sqrt{6}$米,则旗杆的高度为30米.