题目内容
3.抛物线C:y2=4x的焦点为F,N为准线上一点,M为y轴上一点,∠MNF为直角,若线段MF的中点E在抛物线C上,则△MNF的面积为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $3\sqrt{2}$ |
分析 根据抛物线的性质和直角三角形的性质可知NE∥x轴,从而可得E点坐标,求出M、N的坐标,计算MN,NF即可求出三角形的面积.
解答 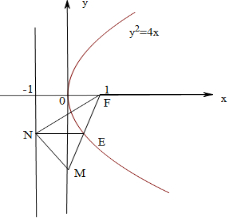 解:准线方程为x=-1,焦点为F(1,0),
解:准线方程为x=-1,焦点为F(1,0),
不妨设N在第三象限,
∵∠MNF为直角,E是MF的中点,
∴NE=$\frac{1}{2}$MF=EF,
∴NE∥x轴,又E为MF的中点,E在抛物线y2=4x上,
∴E($\frac{1}{2}$,-$\sqrt{2}$),∴N(-1,-$\sqrt{2}$),M(0,-2$\sqrt{2}$),
∴NF=$\sqrt{6}$,MN=$\sqrt{3}$,
∴S△MNF=$\frac{1}{2}MN•NF$=$\frac{3\sqrt{2}}{2}$.
故选C.
点评 本题考查了抛物线的简单性质,属于中档题.

练习册系列答案
相关题目
13.在棱长为4的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM和CN所成的角的余弦值是( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
18.已知等比数列{an}满足a1+a3=10,a2+a4=5,则a5=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | 4 |
8.函数$f(x)=cos({ωx+\frac{π}{6}})$(ω>0)的最小正周期为π,则f(x)满足( )
| A. | 在$({0,\frac{π}{3}})$上单调递增 | B. | 图象关于直线$x=\frac{π}{6}$对称 | ||
| C. | $f({\frac{π}{3}})=\frac{{\sqrt{3}}}{2}$ | D. | 当$x=\frac{5π}{12}$时有最小值-1 |
 ,则集合
,则集合 的子集个数为( )
的子集个数为( ) C.8 D.
C.8 D.