题目内容
13.在棱长为4的正方体ABCD-A1B1C1D1中,M和N分别为A1B1和BB1的中点,那么直线AM和CN所成的角的余弦值是( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直线坐标系,利用向量法能求出直线AM和CN所成的角的余弦值.
解答 解: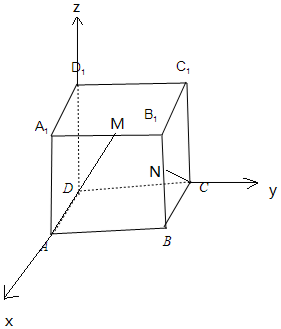 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直线坐标系,
以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直线坐标系,
则A(4,0,0),M(4,2,4),C(0,4,0),N(4,4,2),
$\overrightarrow{AM}$=(0,2,4),$\overrightarrow{CN}$=(4,0,2),
设直线AM和CN所成的角为θ,
则cosθ=$\frac{|\overrightarrow{AM}•\overrightarrow{CN}|}{|\overrightarrow{AM}|•|\overrightarrow{CN}|}$=$\frac{8}{\sqrt{20}•\sqrt{20}}$=$\frac{2}{5}$.
∴直线AM和CN所成的角的余弦值是$\frac{2}{5}$.
故选:D.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
3.已知各项均为正数的等比数列{an}的前n项和为Sn,且S3=14,a3=8,则a6=( )
| A. | 16 | B. | 32 | C. | 64 | D. | 128 |
4.在△ABC中,角A,B,C的对边分别为a,b,c,若a2+c2-b2=3actanB,则角B的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$或$\frac{5π}{6}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
2.若集合A={x|x>$\frac{1}{2}$或x<0},集合B={x|(x+1)(x-2)<0},则A∩B等于( )
| A. | {x|$\frac{1}{2}$<x<2} | B. | {x|-1<x<0或$\frac{1}{2}$<x<2} | C. | {x|-1<x<$\frac{1}{2}$} | D. | {x|0<x<$\frac{1}{2}$或1<x<2} |
3.抛物线C:y2=4x的焦点为F,N为准线上一点,M为y轴上一点,∠MNF为直角,若线段MF的中点E在抛物线C上,则△MNF的面积为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3\sqrt{2}}}{2}$ | D. | $3\sqrt{2}$ |
