题目内容
11.过点P(1,-3)的直线既与抛物线y=x2相切,又与圆(x-2)2+y2=5相切,则切线的斜率为( )| A. | -6 | B. | -2 | C. | -1 | D. | 3 |
分析 设切线切抛物线y=x2于点(a,a2),求出求出的斜率,得到切线方程,利用切线与圆相切,判断切线的斜率即可.
解答 解:设切抛物线y=x2于点(a,a2)可得y′=2x$⇒{k_切}=2a=\frac{{{a^2}+3}}{a-1}⇒{a^2}-2a-3=0⇒a=3或a=-1$,a=3时,切线方程为y=6x-9不与圆相切,所以a=3(舍去),
当a=-1时,切线方程为y=-2x-1与圆相切,因此a=-1成立,
这时K切=-2,
故选:B.
点评 本题考查抛物线的简单性质的应用,切线方程的求法,直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
相关题目
19.设函数f(x)=ex(x3-a)(a∈R)在(-3,0)单调递减,则a的范围是( )
| A. | [0,+∞) | B. | [2,4] | C. | [4,+∞) | D. | (2,4) |
16.某学校为了制定治理学校门口上学、方向期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
(Ⅰ)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序.在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(Ⅱ)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子.现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为ξ,求ξ的分布列和数学期望.
| 同意限定区域停车 | 不同意限定区域停车 | 合计 | |
| 男 | 18 | 7 | 25 |
| 女 | 12 | 13 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅱ)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子.现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为ξ,求ξ的分布列和数学期望.
3.若a∈[1,6],则函数$y=\frac{{{x^2}+a}}{x}$在区间[2,+∞)内单调递增的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
20.2014年5月12日,国家统计局公布了《2013年农民工监测调查报告》,报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图1,并将人均月收入绘制成如图2的不完整的条形统计图.
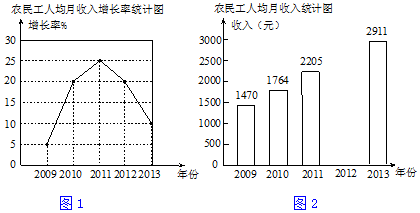
根据以上统计图来判断以下说法错误的是( )

根据以上统计图来判断以下说法错误的是( )
| A. | 2013年农民工人均月收入的增长率是10% | |
| B. | 2011年农民工人均月收入是2205元 | |
| C. | 小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了” | |
| D. | 2009年到2013年这五年中2013年农民工人均月收入最高 |
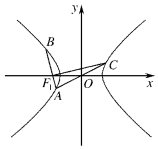 如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.
如图,过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a,b>0)左焦点F1的直线交双曲线左支于A,B两点,C是双曲线右支上一点,且A,C在x轴的异侧,若满足|OA|=|OF1|=|OC|,|CF1|=2|BF1|,则双曲线的离心率为$\frac{\sqrt{17}}{3}$.