题目内容
8.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且满足$\sqrt{3}ccos(2016π-B)-sin(2017π+C)=0$.(1)求角B的大小;
(2)若动点D在△ABC的外接圆上,且点D,B不在AC的同一侧,AC=7,试求△ACD面积的最大值.
分析 (1)根据诱导公式和和正弦定理即可求出,
(2)根据余弦定理和基本不等式以及三角形的面积公式计算即可.
解答 解:(1)在△ABC中,∵$\sqrt{3}ccos(2016π-B)-bsin(2017π+C)=0$,
∴$\sqrt{3}ccosB+bsinC=0$,
由正弦定理,得$\sqrt{3}sinCcosB+sinBsinC=0$,
又0<C<π,
∴sinC≠0,
∴$\sqrt{3}ccosB+bsinC=0$,
即$tanB=-\sqrt{3}$,
又0<B<π,
∴$B=\frac{2π}{3}$.
(2)由点D在△ABC的外接圆上,B,D不在AC的同侧,得$∠D=π-∠B=\frac{π}{3}$,
在△ACD中,由余弦定理,得AC2=AD2+CD2-2AD•CDcosD≥2AD•CD(1-cosD)=AD•CD,即49≥AD•CD,当且仅当AD=CD时,取等号.
∴△ACD的面积$S=\frac{1}{2}AD•CDsinD≤\frac{1}{2}×49sin\frac{π}{3}=\frac{{49\sqrt{3}}}{4}$.
点评 本题考查了正弦定理和余弦定理和三角形的面积公式以及三角函数的化简,考查了学生的运算能力,属于中档题

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
18.复数z=|($\sqrt{3}$-i)i|+i2017(i为虚数单位),则复数z的共轭复数为( )
| A. | 2-i | B. | 2+i | C. | 4-i | D. | 4+i |
19.设函数f(x)=ex(x3-a)(a∈R)在(-3,0)单调递减,则a的范围是( )
| A. | [0,+∞) | B. | [2,4] | C. | [4,+∞) | D. | (2,4) |
16.某学校为了制定治理学校门口上学、方向期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查.根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
(Ⅰ)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序.在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(Ⅱ)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子.现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为ξ,求ξ的分布列和数学期望.
| 同意限定区域停车 | 不同意限定区域停车 | 合计 | |
| 男 | 18 | 7 | 25 |
| 女 | 12 | 13 | 25 |
| 合计 | 30 | 20 | 50 |
(Ⅱ)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子.现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为ξ,求ξ的分布列和数学期望.
3.若a∈[1,6],则函数$y=\frac{{{x^2}+a}}{x}$在区间[2,+∞)内单调递增的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
13.“a>0”是“$a+\frac{2}{a}≥2\sqrt{2}$”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.2014年5月12日,国家统计局公布了《2013年农民工监测调查报告》,报告显示:我国农民工收入持续快速增长.某地区农民工人均月收入增长率如图1,并将人均月收入绘制成如图2的不完整的条形统计图.
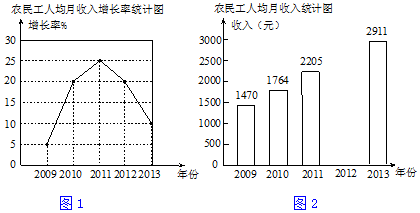
根据以上统计图来判断以下说法错误的是( )

根据以上统计图来判断以下说法错误的是( )
| A. | 2013年农民工人均月收入的增长率是10% | |
| B. | 2011年农民工人均月收入是2205元 | |
| C. | 小明看了统计图后说:“农民工2012年的人均月收入比2011年的少了” | |
| D. | 2009年到2013年这五年中2013年农民工人均月收入最高 |
17.已知$sin(α-\frac{π}{12})=\frac{1}{3}$,则$cos(α+\frac{5π}{12})$的值等于( )
| A. | $\frac{1}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{{2\sqrt{2}}}{3}$ |
18.某学校门前的树上挂了两串彩灯.这两串彩灯的第一次闪亮相互独立,若都在通电后的4秒内任一时刻等可能发生,然后每串彩灯以2秒为间隔闪亮.那么这两串彩灯同时通电后,它们第一次闪亮的时刻相差不超过1秒的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |