题目内容
9.已知函数f(x)=sinxcosx+2,x∈R.(1)求函数f(x)的最大值和最小正周期;
(2)求函数f(x)的单调递增区间.
分析 (1)将f(x)变形为:$f(x)=\frac{1}{2}sin2x+2$,求出f(x)的最大值和f(x)周期T即可;(2)根据正弦函数的单调性求出函数的递增区间即可.
解答 解:f(x)=sinxcosx+2=$f(x)=\frac{1}{2}sin2x+2$,
(1)$f{(x)_{max}}=\frac{1}{2}+2=\frac{5}{2}$,f(x)的最小正周期$T=\frac{2π}{2}=π$.
(2)由$2kπ-\frac{π}{2}≤2x≤2kπ+\frac{π}{2}$得$kπ-\frac{π}{4}≤x≤kπ+\frac{π}{4}$,
∴f(x)的单调递增区间为$[kπ-\frac{π}{4},kπ+\frac{π}{4}],k∈Z$.
点评 本题考查了三角函数的最值以及函数的周期,考查函数的单调性问题,是一道基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
19.正方体ABCD-A1B1C1D1中,与对角线A1B成45°的棱有( )条.
| A. | 4 | B. | 8 | C. | 12 | D. | 2 |
17.某个单位共有职工500人,其中青年职工125人,中年职工280人,老年职工95人.为了了解这个单位职工的身体职工,采用分层抽样的方法从中抽取一个容量为100的样本,则中年职工中应抽取的人数为( )
| A. | 54 | B. | 55 | C. | 56 | D. | 57 |
4.函数y=(3-x2)ex的单调递增区间是( )
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,-3) | D. | (-3,1) |
14.已知实数x,y满足$\left\{{\begin{array}{l}{x+y≥4}\\{x-y≤2}\\{3y-x≤4}\end{array}}\right.$,则$\frac{y}{x}$的最小值为( )
| A. | 1 | B. | $\frac{1}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{4}$ |
1.某一算法框图如图,输出的S值为( )
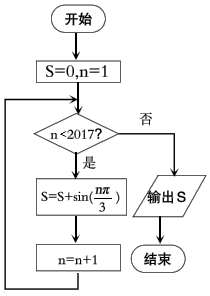

| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\sqrt{3}$ | D. | 0 |
18.双曲线$\frac{x^2}{2}-\frac{y^2}{4}=1$渐近线的斜率为( )
| A. | $±\frac{{\sqrt{2}}}{2}$ | B. | $±\frac{1}{2}$ | C. | $±\sqrt{2}$ | D. | ±2 |