题目内容
17.某个单位共有职工500人,其中青年职工125人,中年职工280人,老年职工95人.为了了解这个单位职工的身体职工,采用分层抽样的方法从中抽取一个容量为100的样本,则中年职工中应抽取的人数为( )| A. | 54 | B. | 55 | C. | 56 | D. | 57 |
分析 分层抽样应按各层所占的比例从总体中抽取,即可得出结论.
解答 解:分层抽样应按各层所占的比例从总体中抽取.
∵职工500人,其中青年职工125人,中年职工280人,老年职工95人,
∴从中抽取一个容量为100的样本,则中年职工中应抽取的人数为$\frac{100}{500}×280$=56人.
故选C.
点评 本题主要考查分层抽样,分层抽样的优点是:使样本具有较强的代表性,并且抽样过程中可综合选用各种抽样方法,因此分层抽样是一种实用、操作性强、应用比较广泛的抽样方法.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目
8.如图,给出的是计算$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2016}$的值的程序框图,其中判断框内可填入的是( )
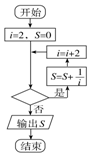

| A. | i≤2 021? | B. | i≤2 019? | C. | i≤2 017? | D. | i≤2 015? |
5.已知两个向量$\overrightarrow a=(cosθ,sinθ),\overrightarrow b=(\sqrt{3},-1)$,则$|{2\overrightarrow a-\overrightarrow b}|$的最大值是( )
| A. | 2 | B. | $2\sqrt{2}$ | C. | 4 | D. | $4\sqrt{2}$ |
2.已知A为△ABC的内角,向量$\overrightarrow m=(\sqrt{3},-1),\overrightarrow n=(cosA,sinA)$,若$\overrightarrow m⊥\overrightarrow n$,则角A=( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
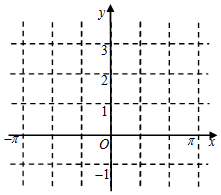 已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)+1(其中0<ω<1),若点(-$\frac{π}{6}$,1)是函数f(x)图象的一个对称中心,
已知函数f(x)=2sin(2ωx+$\frac{π}{6}$)+1(其中0<ω<1),若点(-$\frac{π}{6}$,1)是函数f(x)图象的一个对称中心,