题目内容
以下命题正确的个数为( )
①命题“若x2>1,则x>1”的否命题为“若x2≤1,则x≤1”;
②命题“若α>β,则tanα>tanβ”的逆命题为真命题;
③命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R;都有x2+x+1≥0”;
④“x>1”是“x2+x-2<0”的充分不必要条件.
①命题“若x2>1,则x>1”的否命题为“若x2≤1,则x≤1”;
②命题“若α>β,则tanα>tanβ”的逆命题为真命题;
③命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R;都有x2+x+1≥0”;
④“x>1”是“x2+x-2<0”的充分不必要条件.
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:本题考查的知识点是判断命题真假,比较综合的考查了不等式,正切以及充要条件的一些性质,我们可以根据相应的性质对四个结论逐一进行判断,可以得到正确的结论.
解答:
解;命题的否命题分别否定命题的条件和结论,①正确;
命题“若α>β,则tanα>tanβ”的逆命题为“若tanα>tanβ,则α>β”为假命题,②错误;
特称命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,都有x2+x+1≥0”,③正确;
x2+x-2<0?(x+2)(x-1)<0?“-2<x<1”,“x>1”是“-2<x<1”的既不充分也不必要条件,④错误.
故选:B
命题“若α>β,则tanα>tanβ”的逆命题为“若tanα>tanβ,则α>β”为假命题,②错误;
特称命题“?x∈R,使得x2+x+1<0”的否定是“?x∈R,都有x2+x+1≥0”,③正确;
x2+x-2<0?(x+2)(x-1)<0?“-2<x<1”,“x>1”是“-2<x<1”的既不充分也不必要条件,④错误.
故选:B
点评:④“x>1”是“x2+x-2<0”的充分不必要条件,需要对“x2+x-2<0”化简,同时分别就充分性和必要性做出判断.

练习册系列答案
相关题目
下述函数中,在(-∞,0]内为增函数的是( )
| A、y=x2-2 | ||
B、y=
| ||
| C、y=1+2x | ||
| D、y=-(x+2)2 |
若A∈α,B∈α,A∈l,B∈l,P∈l,则( )
| A、P?α | B、P∉α |
| C、l?α | D、P∈α |
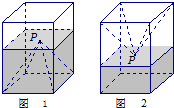 如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题:
如图1,一个正四棱柱形(底面是正方形)的密闭容器底部镶嵌了同底的正四棱锥形实心装饰块(内部不渗水),容器内盛有a升水时,水面恰好经过正四棱锥的顶点P.如果将容器倒置,水面也恰好过点P(图2).有下列四个命题: