题目内容
13．若关于x方程32x-2a•3x+4=0有两个不同的正根，求实数a的取值范围．分析 利用根的判别式、韦达定理及指数函数性质求解．
解答 解：∵关于x方程32x-2a•3x+4=0有两个不同的正根，
∴（3x）2-2a•（3x）+4=0的两个解${3}^{{x}_{1}}$，${3}^{{x}_{2}}$都大于1，
∴$\left\{\begin{array}{l}{△（-2a）^{2}-16＞0}\\{{3}^{{x}_{1}}+{3}^{{x}_{2}}=2a＞2}\end{array}\right.$，
解得a＞2．
∴实数a的取值范围是（2，+∞）．
点评 本题考查实数的取值范围的求法，是基础题，解题时要认真审题，注意根的判别式、韦达定理及指数函数性质的合理运用．
练习册系列答案
相关题目
3．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$满足$\overrightarrow{a}$•（$\overrightarrow{b}$+$\overrightarrow{a}$）=2，且|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{6}$ | D． | $\frac{2π}{3}$ |
4．
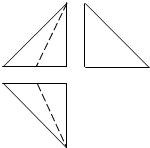如图是一个四面体的三视图，这个三视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为（ ）
如图是一个四面体的三视图，这个三视图均是腰长为2的等腰直角三角形，正视图和俯视图中的虚线是三角形的中线，则该四面体的体积为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{4}{3}$ | C． | $\frac{8}{3}$ | D． | 2 |
8．某班分成8个小组，每小组5人，现要从中选出4人进行4个不同的化学实验，且每组至多选一人，则不同的安排方法种数是（ ）
| A． | ${C}_{8}^{4}$${A}_{4}^{4}$ | B． | ${C}_{8}^{4}$${A}_{4}^{4}$${C}_{5}^{1}$ | C． | 54${C}_{8}^{4}$${A}_{4}^{4}$ | D． | ${C}_{40}^{4}$${A}_{4}^{4}$ |