题目内容
1.与函数y=$\frac{1}{\sqrt{x-1}}$的定义域相同的函数是( )| A. | y=$\sqrt{x-1}$ | B. | y=2x-1 | C. | y=$\frac{1}{x-1}$ | D. | y=ln(x-1) |
分析 求出函数y=$\frac{1}{\sqrt{x-1}}$的定义域,再分别求出选项中的函数定义域,进行判断即可.
解答 解:函数y=$\frac{1}{\sqrt{x-1}}$的定义域是(1,+∞);
对于A,函数y=$\sqrt{x-1}$的定义域是[1,+∞),与已知函数的定义域不同;
对于B,函数y=2x-1的定义域是(-∞,+∞),与已知函数的定义域不同;
对于C,函数y=$\frac{1}{x-1}$的定义域是(-∞,1)∪(1,+∞),与已知函数的定义域不同;
对于D,函数y=ln(x-1)的定义域是(1,+∞),与已知函数的定义域相同.
故选:D.
点评 本题考查了求基本初等函数定义域的应用问题,是基础题目.

练习册系列答案
相关题目
11.已知圆O1:x2+y2-4x+4y-41=0,圆O2:(x+1)2+(y-2)2=4,则两圆的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
16.已知函数f(x)=$\left\{\begin{array}{l}{|lo{g}_{2}x|,0<x≤2}\\{2-lo{g}_{2}x,x>2}\end{array}\right.$若a,b,c互不相等,且f(a)=f(b)=f(c),则ab+bc+ca的取值范围是( )
| A. | (1,4) | B. | (2,4) | C. | (6,9) | D. | (7,9) |
10.经过两点$A({-1,\sqrt{3}})$,$B({1,-\sqrt{3}})$的直线的倾斜角为( )
| A. | 120° | B. | 150° | C. | 60° | D. | 30° |
11.正弦函数y=sinx的图象上最高点和最低点之间的最短距离是( )
| A. | 2 | B. | 2$\sqrt{2}$ | C. | $\sqrt{4+{π}^{2}}$ | D. | 2$\sqrt{1+{π}^{2}}$ |
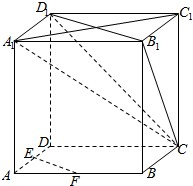 如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、AD的中点.